Question

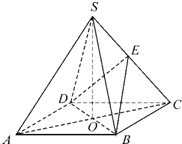如图，在四棱锥S-ABCD中，底面ABCD是正方形，四个侧面都是等边三角形，AC与BD交于点O，E为侧棱SC上的一点．
（1）求证：平面BDE⊥平面SAC；
（2）若SA∥平面BDE，求SE：EC的值．

Answer 1

分析：（1）因为 SB=SD，O是BD中点，所以BD⊥SO，因为四边形ABCD是正方形，所以BD⊥AC，因为AC∩SO=O，所以BD⊥平面SAC．由此能够证明平面BDE⊥平面SAC．
（2）连接OE，由SA∥OE，由此能够证明OE是△ACS的中位线，由此能求出SE：EC的值．

解答：解：（1）因为SB=SD，O是BD中点，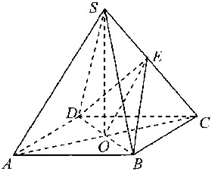
所以BD⊥SO，（1分）
又因为四边形ABCD是正方形，所以BD⊥AC，（3分）
因为AC∩SO=O，所以BD⊥平面SAC．（4分）
又因为BD?平面BDE，
所以平面BDE⊥平面SAC．（6分）
（2）连接OE，则OE?平面BDE，
∵SA∥平面BDE，
∴SA∥OE．
∵ABCD是正方形，AC与BD交于点O，E为侧棱SC上的一点，
∴OE是△ACS的中位线，
∴SE：EC=1．

点评：本题考查平面和平面垂直的证明，考查直线与平面平行的关系的应用，解题时要认真审题，仔细解答，注意把空间几何问题转化为平面几何问题进行求解．