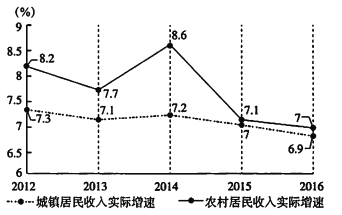
题目内容
【题目】过点
的直线
与
轴正半轴和
轴正半轴分别交于
，
（1）当
为
的中点时，求的方程
（2）当
最小时，求的方程
（3）当
面积取到最小值时，求的方程
【答案】（1）
（2）
（3）
【解析】
（1）设
，
，由
为
的中点，求出
，再写方程. （2）设所求直线的方程为
，求出
，
，表示出
，用均值定理即可
（3）设直线的截距式方程为
，由
用均值定理即可.
解：（1）设，，
∵
为的中点，
∴
，
，
∴由截距式得
的方程为：
，
即；
（2）设所求直线的方程为，由题意知
，
令
可得
，令
可得
，
即，.
∴
，
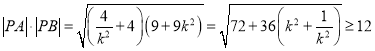当且仅当
，即
时取等号，取最小值为12，
即直线的方程为；
（3）由题意设直线的截距式方程为，
∵直线过，
∴，
∴
，∴
.
当且仅当
即
且
时取等号，
∴
的面积
，
∴面积的最小值为12，此时直线的方程为
，
即直线的方程为.
练习册系列答案
相关题目
