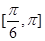题目内容
已知|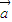 |=2|
|=2|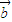 |≠0,且关于x的函数f(x)=
|≠0,且关于x的函数f(x)= x3+
x3+ |
| |x2+
|x2+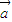 •
•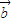 x在R上有极值,则
x在R上有极值,则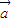 与
与 的夹角范围为 .
的夹角范围为 .
【答案】分析:根据函数在实数上有极值求出导函数,使得导函数等于零有解,即一元二次方程有解,判别式大于零,得到 的模与两向量数量积的不等关系,把不等关系代入夹角公式,得到夹角余弦的范围,求出角的范围.
的模与两向量数量积的不等关系,把不等关系代入夹角公式,得到夹角余弦的范围,求出角的范围.
解答:解:∵f′(x)=x2+| |x+
|x+ ,
,
∵函数在实数上有极值,
∴△= >0,
>0,
∴4 ,
,
∵cosθ= <
< ,
,
∴ ,
,
故答案为:( )
)
点评:启发学生在理解数量积的运算特点的基础上,逐步把握数量积的运算律,引导学生注意数量积性质的相关问题的特点,以熟练地应用数量积的性质.?
 的模与两向量数量积的不等关系,把不等关系代入夹角公式,得到夹角余弦的范围,求出角的范围.
的模与两向量数量积的不等关系,把不等关系代入夹角公式,得到夹角余弦的范围,求出角的范围.解答:解:∵f′(x)=x2+|
 |x+
|x+ ,
,∵函数在实数上有极值,
∴△=
 >0,
>0,∴4
 ,
,∵cosθ=
 <
< ,
,∴
 ,
,故答案为:(
 )
)点评:启发学生在理解数量积的运算特点的基础上,逐步把握数量积的运算律,引导学生注意数量积性质的相关问题的特点,以熟练地应用数量积的性质.?

练习册系列答案
相关题目
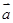 |=2|
|=2|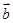 |≠0,且关于x的方程x2+|
|≠0,且关于x的方程x2+|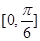 B.
B.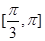 C.
C.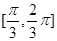 D.
D.