题目内容
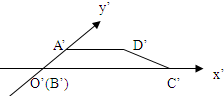已知梯形ABCD是直角梯形，按照斜二测画法画出它的直观图A′B′C′D′如图所示，其中A′D′=2，B′C′=4，A′B′=1，则直角梯形以BC为旋转轴旋转一周形成的几何体的体积为| 32π |
| 3 |
| 32π |
| 3 |
分析：根据题意将图形还原，得下底为4、高与直角腰都等于2的直角梯形，从而得到所求旋转体是由一个圆柱和一个圆锥两部分构成，再结合圆柱、圆锥的体积公式，即可得到所求的体积．
解答：解：根据题意，四边形A′B′C′D′还原成梯形直角梯形ABCD如图，
得AB=AD=2，BC=4
∴直角梯形以BC为旋转轴旋转一周，形成的几何体由底面半径和高均为2圆柱，
和底面半径为2，高等于2的圆锥两部分构成，
由此可得，所求的体积为：V=π×22×2+
×π×22×2=
故答案为：
得AB=AD=2，BC=4
∴直角梯形以BC为旋转轴旋转一周，形成的几何体由底面半径和高均为2圆柱，
和底面半径为2，高等于2的圆锥两部分构成，
由此可得，所求的体积为：V=π×22×2+
| 1 |
| 3 |
| 32π |
| 3 |
故答案为：
| 32π |
| 3 |
点评：本题给出直角梯形，求以它的下底旋转而成的几何体的体积，着重考查了斜二侧画法、圆柱体积与圆锥体积的求法等知识点，属于中档题．
练习册系列答案
科学实验活动册系列答案
相关题目
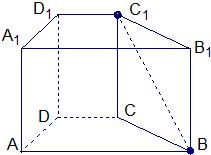
如图，在等腰梯形ABCD中，M，N分别是AB，CD的中点，沿MN将MNCB折起至MNC1B1，使它与MNDA成直二面角．已知AB=2CD=4MN，给出下列四个等式：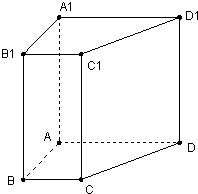
已知直四棱柱ABCD-A1B1C1D1，底面四边形ABCD是一个直角梯形，上底边长BC=2，下底边长AD=6，直角边所在的腰AB=2，体积V=48．求直线B1D 与平面ABB1A1所成的角α（用反三角函数表示）．
（本小题满分12分）如图1，已知四边形ABCD是上、下底边长分别为2和6，高为
的等腰梯形，将它沿对称轴OO1折成直二面角，如图2.
（Ⅱ）求二面角O－AC－O1的大小. 