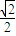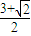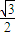题目内容
已知某空间几何体的主视图、侧视图、俯视图均为等腰直角三角形,如果直角三角形的直角边长为2,那么这个几何体的表面积可以是
6+2
或4+4
| 3 |
| 2 |
6+2
或4+4
.| 3 |
| 2 |
分析:首先确定三个视图全为等腰直角三角形的几何体的结构特点,再分别求表面积
解答:解:能使得主视图、侧视图、俯视图均为等腰直角三角形的几何体可能有如图两种三棱锥


图1 图2
图1中,OA,AB,AC两两垂直,
图2中,PD⊥面DEF,DE⊥EF
由题意知:
图1中,OA=AB=AC=2,∴△OBC是边长为2
的等边三角形
∴表面积为S=3×
×2×2+
×(2
)2=6+2
图2中,PD=DE=EF=2
∵PD⊥面DEF
∴PD⊥EF
又∵DE⊥EF且PD∩DE=D
∴EF⊥面PDE
∴EF⊥PE
∴△PEF是直角三角形
∴表面积为S=S△DEF+S△PDE+S△PDF+S△PEF=
×2×2+
×2×2+
×2
×2+
×2×2
=4+4
故答案为:6+2
或4+4


图1 图2
图1中,OA,AB,AC两两垂直,
图2中,PD⊥面DEF,DE⊥EF
由题意知:
图1中,OA=AB=AC=2,∴△OBC是边长为2
| 2 |
∴表面积为S=3×
| 1 |
| 2 |
| ||
| 4 |
| 2 |
| 3 |
图2中,PD=DE=EF=2
∵PD⊥面DEF
∴PD⊥EF
又∵DE⊥EF且PD∩DE=D
∴EF⊥面PDE
∴EF⊥PE
∴△PEF是直角三角形
∴表面积为S=S△DEF+S△PDE+S△PDF+S△PEF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
故答案为:6+2
| 3 |
| 2 |
点评:本题考查由三视图求面积,要求有比较好的空间想象力,能够把三视图还原成原来的几何体,并且能找到几何体中的线段的位置关系和长度关系.属简单题

练习册系列答案
相关题目
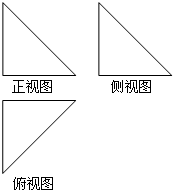 已知某空间几何体的主视图、侧视图、俯视图均为如图所示的等腰直角三角形,如果直角三角形的直角边长为1,那么这个几何体的表面积为( )
已知某空间几何体的主视图、侧视图、俯视图均为如图所示的等腰直角三角形,如果直角三角形的直角边长为1,那么这个几何体的表面积为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
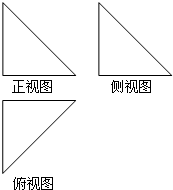
 已知某空间几何体的主视图、侧视图、俯视图均为如图所示的等腰直角三角形,如果直角三角形的直角边长为1,那么这个几何体的表面积为( )
已知某空间几何体的主视图、侧视图、俯视图均为如图所示的等腰直角三角形,如果直角三角形的直角边长为1,那么这个几何体的表面积为( )