题目内容
如图,AD为△ABC的边BC上的高,E在AD上,且AE=求证:EA′⊥平面A′BC.
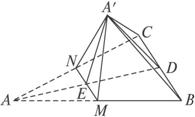
证明:∵AD⊥BC,MN∥BC,∴AD⊥MN,
即AE⊥MN.∴A′E⊥MN.∴A′E⊥BC. ①
如题图,连结A′D,在△A′ED中,设ED=a,A′E=![]() a,
a,
∴A′D2=DE2+EA′2-2ED·EA′cos∠A′ED=a2+![]() a2
a2![]() cos60°=
cos60°=![]() .
.
又ED2=a2,A′E2+A′D2=![]() a2+
a2+![]() ,
,
∴ED2=A′E2+A′D2.∴A′E⊥A′D.
由①知A′E⊥BC,A′D∩BC=D,∴EA′⊥平面A′BC.

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
 如图,在△ABC中,∠BAC=120°,AB=AC=2,D为BC边上的点,且
如图,在△ABC中,∠BAC=120°,AB=AC=2,D为BC边上的点,且 如图,在△ABC中,点D在BC上,且CD=2BD;点E在AC上,且AE=3EC.AD与BE的交点为F.若设
如图,在△ABC中,点D在BC上,且CD=2BD;点E在AC上,且AE=3EC.AD与BE的交点为F.若设 (2012•天河区三模)如图,在△ABC中,AB=3,AC=2,D是边BC的中点,则
(2012•天河区三模)如图,在△ABC中,AB=3,AC=2,D是边BC的中点,则