题目内容
已知函数f（x）＝x3＋ax2＋bx＋1在x＝－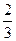
与x＝1时都取得极值。
(1)求a、b的值与函数f（x）的单调区间；
(2)求函数f（x）的单调区间
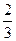与x＝1时都取得极值。(1)求a、b的值与函数f（x）的单调区间；
(2)求函数f（x）的单调区间
解：（1）f（x）＝x3＋ax2＋bx＋1，f¢（x）＝3x2＋2ax＋b--------------（2分）
由f¢（
）＝
，
f¢（1）＝3＋2a＋b＝0
得a＝
，b＝－2---------------------------------------------------------（6分）
f¢（x）＝3x2－x－2＝（3x＋2）（x－1），函数f（x）的单调区间如下表：
-------------------（10分）
所以函数f（x）的递增区间是（－¥，－）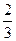
与（1，＋¥）; 递减区间是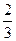（－，1）--------------------------------------------------（12分）
由f¢（
）＝，f¢（1）＝3＋2a＋b＝0
得a＝
，b＝－2---------------------------------------------------------（6分）f¢（x）＝3x2－x－2＝（3x＋2）（x－1），函数f（x）的单调区间如下表：
| x | 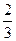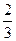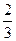（－¥，－） | － | （－，1） | 1 | （1，＋¥） |
| f¢（x） | ＋ | 0 | － | 0 | ＋ |
| f（x） | | 极大值 | ¯ | 极小值 | |
所以函数f（x）的递增区间是（－¥，－
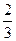）与（1，＋¥）; 递减区间是（－
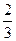，1）--------------------------------------------------（12分） 略
练习册系列答案
相关题目
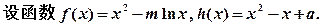
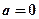时，
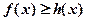在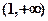
上恒成立，求实数
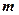的取值范围；
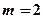时，若函数
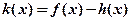在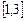
上恰有两个不同零点，求实数
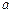的取值范围；
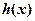在公共定义域上具有相同的单调区间？若存在，求出
，
．
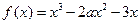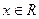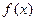在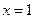
处取得极值，求
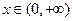时，
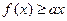恒成立，求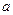
的取值范围．
是定义
在R上的奇函数，当
时，
，且
，
的解集为 ▲ 
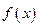为定义在R上的偶函数，且导数
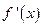存在，则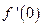
的值为 ( ▲ )
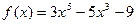的极值点的个数( ▲ )
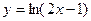上的点到直线
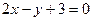的最短距离是（ ）
