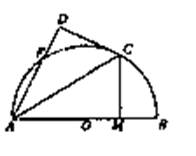
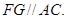题目内容
(本小题满分22分)
将m位性别相同的客人,按如下方法入住A1、A2、…、A n共n个房间。首先,安排1位客人和余下的客人![]() 的入住房间A1;然后,从余下的客人中安排2位和再次余下的客人
的入住房间A1;然后,从余下的客人中安排2位和再次余下的客人![]() 的入住房间A2;依此类推,第几号房间就安排几位客人和余下的客人
的入住房间A2;依此类推,第几号房间就安排几位客人和余下的客人![]() 的入住;这样,最后一间房间A n正好安排最后余下的n位客人。试求客人的数目和客房的数目,以及每间客房入住客人的数目。
的入住;这样,最后一间房间A n正好安排最后余下的n位客人。试求客人的数目和客房的数目,以及每间客房入住客人的数目。
解析:设安排完第k号客房A k后还剩下a k位客人,则a0=m,an-1= n…(4分)
因为第k号客房A k入住的客人数为![]() ,
,
所以![]()
![]() ,即
,即![]() ……………………(8分)
……………………(8分)
变形得![]() .
.
这表明数列b k=a k+6k-36是等比数列,公比q=![]() ,
,
其中b0=a 0-36=m-36,bn-l= a n-l+6 (n-1)-36=7n一42. ……(12分)
代入通项公式得7n一42=![]() ,
,
即 ![]() ………………(16分)
………………(16分)
由于m为正整数, 并且![]() 与
与![]() 互质,故
互质,故![]() |(n一6),
|(n一6),
但 ![]()
解得n=6,从而m=36.………………………………………………(20分)
由此可知,客房A1入住l+![]() = 6位客人;客房A2入住2+
= 6位客人;客房A2入住2+![]() =6位客人;客房A3入住3+
=6位客人;客房A3入住3+![]() =6位客人;客房A4入住4+
=6位客人;客房A4入住4+![]() =6位客人;客房A5人住5+
=6位客人;客房A5人住5+![]() =6位客人;最后一间客房人住了剩下的6位客人.
=6位客人;最后一间客房人住了剩下的6位客人.
综上可知,共有客人36人,客房6间,每间客房均入住6位客人.…(22分)

练习册系列答案
相关题目
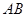 是⊙O的一条切线,切点为
是⊙O的一条切线,切点为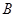 ,
,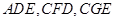 都是⊙O的割线,已知
都是⊙O的割线,已知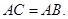 证明:
证明: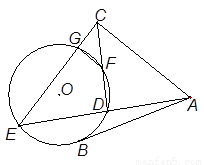
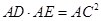 ;
;