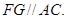题目内容
(本小题满分22分)
设A、B分别为椭圆![]()
![]() 和双曲线
和双曲线![]() 的公共的左、右顶点。P、Q分别为双曲线和椭圆上不同于A、B的动点,且满足
的公共的左、右顶点。P、Q分别为双曲线和椭圆上不同于A、B的动点,且满足![]()
![]() 。设直线AP、BP、AQ、BQ的斜率分别为k1、k2、k3、k4.
。设直线AP、BP、AQ、BQ的斜率分别为k1、k2、k3、k4.
(1)求证:k1+k2+k3+k4=0;
(2)设 F1、F2分别为椭圆和双曲线的右焦点。若![]() ,求
,求![]() 的值。
的值。
解析:(1)设P、Q两点的坐标分别为P(x1,y1),Q(x2,y2),则
k1+k2=![]() ①……………(4分)
①……………(4分)
同理可得意k3+k4=![]() ② …………………………(7分)
② …………………………(7分)
设O为原点,则![]() ,
,
所以![]() ,O,P,Q三点共线,于是得
,O,P,Q三点共线,于是得![]() .
.
由①②得 kl+k2+k3+k4=0; ………………………………………(11分)
(2) 由点Q在椭圆上,有![]() =1.
=1.
由 ![]() ,得(xl,y1)=
,得(xl,y1)=![]() (x2,y2).
(x2,y2).
所以 x2=![]() x l,y2=
x l,y2=![]() y l,从而
y l,从而![]() =
=![]() 2 ③
2 ③
又由点P在双曲线上,有![]() =1 ④
=1 ④
由③④得 ![]() ……………………(15分)
……………………(15分)
因为PF2∥QF1,所以| OF2|=![]() |OF1| ,所以
|OF1| ,所以
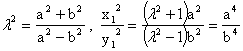 ………………………………(18分)
………………………………(18分)
由①得 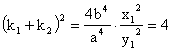 .同理可得
.同理可得 ![]() .另一方面,
.另一方面,
klk2=![]() .类似地,k3k4=
.类似地,k3k4=![]() .
.
故![]() -2(klk2+k3k4)=8 …(22分)
-2(klk2+k3k4)=8 …(22分)

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
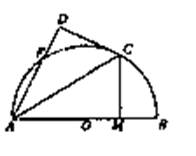
相关题目
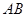 是⊙O的一条切线,切点为
是⊙O的一条切线,切点为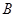 ,
,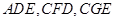 都是⊙O的割线,已知
都是⊙O的割线,已知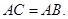 证明:
证明: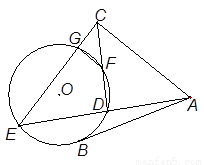
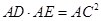 ;
;