Question

【题目】已知0＜α＜π，tanα=﹣2．
（1）求sin（α+ ）的值；
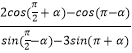（2）求 的值；
（3）2sin2α﹣sinαcosα+cos2α

Answer 1

【答案】
（1）解：因为0＜α＜π，tanα=﹣2，所以sinα= ，cosα=

sin（α+ ）=sinαcos +cosαsin = +（ ）× =

（2）解：原式= = =﹣1
（3）解：原式=

= =

【解析】（1）由已知中0＜α＜π，tanα=﹣2，根据同角三角函数关系，我们可以求出sinα，cosα的值，代入两角和的正弦公式，即可求出sin（α+ ）的值；（2）利用诱导公式，我们可以将原式化为用α的三角函数表示的形式，弦化切后，tanα=﹣2，即可得到答案．（3）根据sin2α+cos2α=1，我们可以将2sin2α﹣sinαcosα+cos2α化为齐次分式，弦化切后，代入tanα=﹣2，即可得到答案．