题目内容

已知向量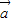=（cosx，2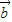），=（sinx，-3）．
（1）当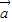∥时，求3cos2x-sin2x的值；
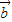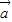（2）求函数f（x）=（-）•在x∈[-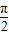，0]上的值域．
【答案】分析：（1）直接根据向量共线对应的结论得到tanx=-，再结合齐次式的应用即可求出结论；
（2）先根据二倍角公式以及辅助角公式对所求函数进行整理，再结合余弦函数的定义域和值域即可求出结论．
解答：解：（1）∵∥时，
∴-3cosx=2sinx，
∴tanx=-．
3cos2x-sin2x===．
（2）f（x）=（-）•=cos2x-sinxcosx+10
=-sin2x+10=cos+．
∵x∈．
∴-≤2x+≤，
∴-≤cos≤，
∴10≤cos+≤，
即f（x）的值域为．
点评：本题主要考查了平面向量数量积的应用，和两角和公式，二倍角公式的运用．三角函数的基本公式较多，注意多积累．
练习册系列答案
相关题目
已知向量
a
=（cosx，sinx），
b
=（-cosx，cosx），
c
=（-1，0）．
（Ⅰ）若x=
π
6
，求向量
a
、
c
的夹角；
（Ⅱ）当x∈[
π
2
，
9π
8
]时，求函数f(x)=2
a
•
b
+1的最大值．
已知向量
m
=(2sinx-cosx，sinx)，
n
=(cosx-sinx，0)，且函数f(x)=(
m
+2
n
)•
m．

（Ⅰ）求函数f（x）的最小正周期；
（Ⅱ）将函数f（x）向左平移
π
4
个单位得到函数g（x），求函数g（x）的单调递增区间．
已知向量
m
=(
3
sinx+cosx，1)，
n
=(
1
2
f(x)，cosx)，
m
∥
n
．
（I）求f（x）的单调增区间及在[-
π
6
，
π
4
]内的值域；
（II）已知A为△ABC的内角，若f(
A
2
)=1+
3
，a=1，b=
2
，求△ABC的面积．
已知向量
m
=(
3
sinx+cosx，1)，
n
=(cosx，-f(x))，且
m
⊥
n
，
（1）求f（x）的单调区间；
（2）当x∈[0， 
π
2
]时，函数g(x)=a[f(x)-
1
2
]+b的最大值为3，最小值为0，试求a、b的值．
已知向量
m
=(
3
sinx-cosx，1)，
n
=(cosx，
1
2
)，若f(x)=
m
•
n
．
（Ⅰ） 求函数f（x）的最小正周期；
（Ⅱ） 已知△ABC的三内角A、B、C的对边分别为a、b、c，且a=3，f(
A
2
+
π
12
)=
3
2
（A为锐角），2sinC=sinB，求A、c、b的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网