Question

已知Max{a，b}=

a，a≥b b，a＜b

，若函数f（x）=Max{|x²-4x|，x}，则函数f（x）（　　）

• A、有最小值为0，有最大值为4
• B、无最小值，有最大值为4
• C、有最小值为0，无最大值
• D、无最值

Answer 1

分析：根据题意画出函数y=|x²-4x|和y=x的图象，容易写出函数f（x）的解析式，得出函数f（x）的最值情况．

解答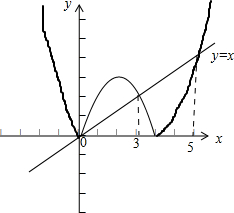：解：根据题意画出函数y=|x²-4x|和y=x的图象，如图所示，；
则y=|x²-4x|=

x2-4x…x≤0或x≥4 -x2+4x…0＜x＜4

，
当x≤3时，f（x）=|x²-4x|，当3＜x＜5时，f（x）=x，当x≥5时，f（x）=|x²-4x|；
即f（x）=

|x2-4x|…x≤3 x…3＜x＜5 |x2-4x|…x≥5

；
∴函数f（x）有最小值f（0）=0，没有最大值．
故选：C．

点评：本题考查了新定义的分段函数的最值问题，可以根据题意画出函数图象，数形结合解答本题，是中档题．