题目内容
已知函数 ,x∈[2,5]
,x∈[2,5]
(1)判断f(x)的单调性并证明;
(2)求f(x)的最大值及最小值.
解:(1)f(x)在[2,5]上单调递增,下面证明:
因为f′(x)= =
=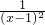 >0,
>0,
所以f(x)在[2,5]上单调递增;
(2)由(1)知f(x)在[2,5]上单调递增,
所以fmin(x)=f(2)= =1,fmax(x)=f(5)=
=1,fmax(x)=f(5)= =
= .
.
故f(x)的最大值为 ,最小值为1.
,最小值为1.
分析:(1)先求出导数f′(x),再根据导数的符号即可判断函数的单调性;
(2)由(1)知f(x)的单调性,借助单调性即可求得其最大值、最小值.
点评:本题考查利用导数研究函数的单调性及求函数在闭区间上的最值问题,准确求导,正确理解导数与函数单调性、最值间的关系是解决问题的基础.
因为f′(x)=
 =
=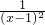 >0,
>0,所以f(x)在[2,5]上单调递增;
(2)由(1)知f(x)在[2,5]上单调递增,
所以fmin(x)=f(2)=
 =1,fmax(x)=f(5)=
=1,fmax(x)=f(5)= =
= .
.故f(x)的最大值为
 ,最小值为1.
,最小值为1.分析:(1)先求出导数f′(x),再根据导数的符号即可判断函数的单调性;
(2)由(1)知f(x)的单调性,借助单调性即可求得其最大值、最小值.
点评:本题考查利用导数研究函数的单调性及求函数在闭区间上的最值问题,准确求导,正确理解导数与函数单调性、最值间的关系是解决问题的基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)=2||log2x|-|x-
|,则不等式f(x)>f(
)的解集等于( )
| 1 |
| x |
| 1 |
| 2 |
A、(
| ||||
B、(
| ||||
C、(-∞,
| ||||
D、(
|