题目内容
 某校从高二年级学生中随机抽取60名学生,将其会考的政治成绩(均为整数)分成六段:[40,50),[50,60),…,[90,100]后得到如下频率分布直方图.
某校从高二年级学生中随机抽取60名学生,将其会考的政治成绩(均为整数)分成六段:[40,50),[50,60),…,[90,100]后得到如下频率分布直方图.(Ⅰ)求图中a的值
(Ⅱ)根据频率分布直方图,估计该校高二年级学生政治成绩的平均分;
(Ⅲ)用分层抽样的方法在80分以上的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任意选取2人,求其中恰有1人的分数不低于90分的概率.
分析:(1)根据所有的基本事件的概率之和等于1,可得a的值.
(2)估计该校高二年级学生政治成绩的平均分为直方图中各个小矩形的宽的中点横坐标乘以小矩形高的10倍,相加所得结果即为所求.
(3)从中抽取6人为样本,则这6人中,分数不低于90的有1人,另外5人的分数位于80至90之间.再从这6人中抽取2人,共有
=15种方法,而满足条件的
抽法有5×1=5种,由此求得恰有1人分数不低于90的概率.
(2)估计该校高二年级学生政治成绩的平均分为直方图中各个小矩形的宽的中点横坐标乘以小矩形高的10倍,相加所得结果即为所求.
(3)从中抽取6人为样本,则这6人中,分数不低于90的有1人,另外5人的分数位于80至90之间.再从这6人中抽取2人,共有
| C | 2 6 |
抽法有5×1=5种,由此求得恰有1人分数不低于90的概率.
解答:解:(1)根据所有的基本事件的概率之和等于1,可得10×(0.01+0.015+0.015+a+0.025+0.005 )=1,解得a=0.03.
(2)估计该校高二年级学生政治成绩的平均分为 45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71.
(3)80分以上的学生共有60×(0.25+0.05)=18人,其中,不低于90分的有60×0.05=3人,分数位于80至90之间的有15人.
从中抽取6人为样本,则这6人中,分数不低于90的有1人,另外5人的分数位于80至90之间.
再从这6人中抽取2人,共有
=15种方法,故恰有1人分数不低于90的概率为
=
.
(2)估计该校高二年级学生政治成绩的平均分为 45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71.
(3)80分以上的学生共有60×(0.25+0.05)=18人,其中,不低于90分的有60×0.05=3人,分数位于80至90之间的有15人.
从中抽取6人为样本,则这6人中,分数不低于90的有1人,另外5人的分数位于80至90之间.
再从这6人中抽取2人,共有
| C | 2 6 |
| 1×5 |
| 15 |
| 1 |
| 3 |
点评:本题主要考查分层抽样的定义和方法,古典概率及其计算公式的应用,属于基础题.

练习册系列答案
相关题目
 ,
, ,…,
,…, 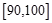 后得到如下频率分布直方图.
后得到如下频率分布直方图.
 内的频率;
内的频率; ,
, ,…,
,…, 后得到如下频率分布直方图.
后得到如下频率分布直方图.
 的值
的值
