题目内容
已知函数 .
.(Ⅰ)求
 的值;
的值;(Ⅱ)若对于任意的
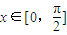 ,都有f(x)≤c,求实数c的取值范围.
,都有f(x)≤c,求实数c的取值范围.
【答案】分析:(Ⅰ)由条件利用二倍角的余弦公式求出 的值.
的值.
(Ⅱ)利用三角恒等变换化简f(x)的解析式为 ,由x的范围求出角
,由x的范围求出角 的范围,可得f(x)的最大值,可得实数c的取值范围.
的范围,可得f(x)的最大值,可得实数c的取值范围.
解答:解:(Ⅰ)∵函数 ,∴
,∴ . …(5分)
. …(5分)
(Ⅱ)∵ …(7分)
…(7分)
= …(8分)
…(8分)
= . …(9分)
. …(9分)
因为 ,所以
,所以  ,…(10分)
,…(10分)
所以当 ,即
,即  时,f(x)取得最大值
时,f(x)取得最大值 . …(11分)
. …(11分)
所以 ,f(x)≤c等价于
,f(x)≤c等价于  .
.
故当 ,f(x)≤c时,c的取值范围是
,f(x)≤c时,c的取值范围是 . …(13分)
. …(13分)
点评:本题主要考查三角函数的恒等变换及化简求值,正弦函数的定义域、值域,属于中档题.
 的值.
的值.(Ⅱ)利用三角恒等变换化简f(x)的解析式为
 ,由x的范围求出角
,由x的范围求出角 的范围,可得f(x)的最大值,可得实数c的取值范围.
的范围,可得f(x)的最大值,可得实数c的取值范围.解答:解:(Ⅰ)∵函数
 ,∴
,∴ . …(5分)
. …(5分)(Ⅱ)∵
 …(7分)
…(7分)=
 …(8分)
…(8分)=
 . …(9分)
. …(9分)因为
 ,所以
,所以  ,…(10分)
,…(10分)所以当
 ,即
,即  时,f(x)取得最大值
时,f(x)取得最大值 . …(11分)
. …(11分)所以
 ,f(x)≤c等价于
,f(x)≤c等价于  .
.故当
 ,f(x)≤c时,c的取值范围是
,f(x)≤c时,c的取值范围是 . …(13分)
. …(13分)点评:本题主要考查三角函数的恒等变换及化简求值,正弦函数的定义域、值域,属于中档题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
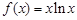 .
.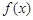 的最小值;
的最小值;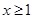 都有
都有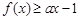 ,求实数
,求实数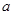 的取值范围.
的取值范围.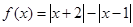
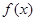 的值域;
的值域;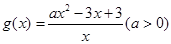 ,若对
,若对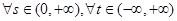 恒有
恒有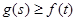 成立,试求实数
成立,试求实数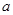 的取值氛围。
的取值氛围。 ,(1)求
,(1)求 的定义域;
的定义域; 是第四象限的角,且
是第四象限的角,且 ,求
,求 的值。
的值。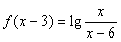 ,
,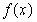 的解析式;
的解析式; .
.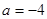 时,求
时,求 的最小值;
的最小值;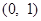 上为单调函数,求实数
上为单调函数,求实数 的取值范围;
的取值范围;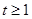 时,不等式
时,不等式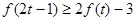 恒成立,求实数
恒成立,求实数