题目内容
已知圆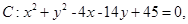 及点
及点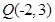 .
.
(1)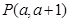 在圆上,求线段
在圆上,求线段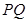 的长及直线
的长及直线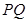 的斜率;
的斜率;
(2)若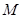 为圆
为圆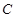 上任一点,求
上任一点,求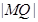 的最大值和最小值;
的最大值和最小值;
(3)若实数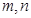 满足
满足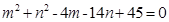 ,求
,求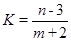 的最大值和最小值.
的最大值和最小值.
【答案】
(1) (2)最小值
(2)最小值 ,最大值
,最大值 (3)
(3) 的最大值为
的最大值为 ,最小值为
,最小值为
【解析】本题考查的知识点是直线和圆的方程的应用,其中将圆C的一般方程,化为标准方程,进而求出圆心坐标及半径是解答本题的关键
(I)由已知中P(a,a+1)在圆C上,代入即可得到一个关于a的一元二次方程,解方程求出满足条件 的a值,代入两点确定直线的斜率公式,即可求出答案.
(II)由已知中圆C:x2+y2-4x-14y+45=0我们可以求出圆的标准方程,进而求出圆心坐标及半径,及CQ的长度,进而得到|MQ|的最大值和最小值.
解:(1)∵ 点P(a,a+1)在圆上,
∴  , ∴
, ∴  , P(4,5),
, P(4,5),
∴  , KPQ=
, KPQ= ,
,
(2)∵ 圆心坐标C为(2,7),
∴  ,
,
∴  ,
, 。
。
(3)设点(-2,3)的直线l的方程为: ,
,
易知直线l与圆方程相切时,K有最值, ∴  ,
,
∴  ∴
∴ 的最大值为
的最大值为 ,最小值为
,最小值为 .
.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
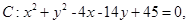 及点
及点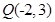 .
. 在圆上,求线段
在圆上,求线段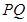 的长及直线
的长及直线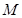 为圆
为圆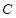 上任一点,求
上任一点,求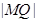 的最大值和最小值;
的最大值和最小值;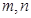 满足
满足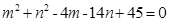 ,求
,求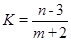 的最大值和最小值.
的最大值和最小值.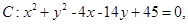 及点
及点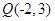 .
.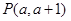 在圆上,求线段
在圆上,求线段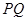 的长及直线
的长及直线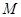 为圆
为圆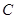 上任一点,求
上任一点,求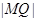 的最大值和最小值;
的最大值和最小值;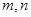 满足
满足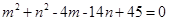 ,求
,求 的最大值和最小值.
的最大值和最小值. 及点
及点 .
. 在圆上,求线段
在圆上,求线段 的长及直线
的长及直线 为圆
为圆 上任一点,求
上任一点,求 的最大值和最小值;
的最大值和最小值; 满足
满足 ,求
,求 的最大值和最小值.
的最大值和最小值.