题目内容
某商场欲经销某种商品，考虑到不同顾客的喜好，决定同时销售
、
两个品牌，根据生产厂家营销策略，结合本地区以往经销该商品的大数据统计分析，品牌的销售利润
与投入资金
成正比，其关系如图1所示，品牌的销售利润
与投入资金的算术平方根成正比，其关系如图2所示（利润与资金的单位：万元）．
（1）分别将、两个品牌的销售利润、表示为投入资金的函数关系式；
（2）该商场计划投入5万元经销该种商品，并全部投入、两个品牌，问：怎样分配这5万元资金，才能使经销该种商品获得最大利润，其最大利润为多少万元？
【解答】： (1) 因为品牌的销售利润与投入资金成正比，设
，
又过点
，所以
，所以
………………3分
品牌的销售利润与投入资金的算术平方根成正比，设
，又过点
，所以
，所以设
， ………………6分
（2）设总利润为
,投入品牌为万元，则投入品牌为
万元，
则
………………8分
令
，则
………………10分
当
时，即
时，投入品牌为：
，
………………13分
答：投入品牌
万元、品牌
万元时，经销该种商品获得最大利润，最大利润为
万元． ……………………14分
练习册系列答案
相关题目
已知函数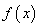
的定义域为
，部分对应值如下表, 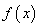的导函数
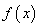的图象如图所示. 下列关于的命题：
|
| －1 | 0 | 4 | 5 |
|
| 1 | 2 | 2 | 1 |
①函数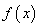的极大值点为
，
；
②函数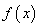在
上是减函数；
③如果当
时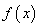，的最大值是2，那么
的最大值为4；
④函数
的零点个数可能为0、1、2、3、4个．其中正确命题的序号是 ．
则
的值为
在区间
上是减函数，则
的取值范围_________
B. 
C. 1 D. 6
，则直线l的斜率是___________.
＝8，
＝5，则
的取值范围是__________．