题目内容
设等差数列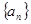 的前
的前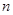 项和为
项和为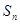 ,且
,且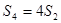 ,
,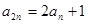 .
.
(1)求数列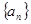 的通项公式;
的通项公式;
(2)设数列 满足
满足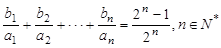 ,求
,求 的通项公式;
的通项公式;
(3)求数列 前
前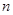 项和
项和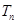 .
.
(1) (2)
(2)  (3)
(3)
解析试题分析:解:(Ⅰ)设等差数列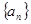 的公差为
的公差为 ,由
,由 ,
, 得
得
解得 ,
,
∴
(Ⅱ)由已知 ,---①
,---①
当 时,
时, ;
;
当 时,
时, ,---②
,---②
将①-②,得 -
- =
= ,
,  ,
,
由(Ⅰ)知 ,∴
,∴
∴检验 ,符合,
,符合,

(3)由已知得 ③,
③, ④
④
将③-④,得,

∴
考点:数列的通项公式;数列的前n项和公式
点评:求一般数列的问题时,常用的方法是裂变法和错位相减法,本题就用到错位相减法。

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
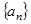 的各项均是正数,其前
的各项均是正数,其前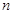 项和为
项和为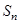 ,满足
,满足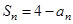 .
.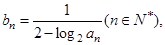 数列
数列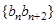 的前
的前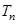 ,求证:
,求证: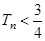 .
.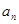 }中,
}中,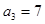 ,又
,又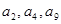 成等比数列.
成等比数列. ,求数列{
,求数列{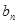 }的前n项和
}的前n项和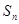 .
.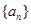 满足
满足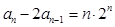
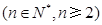 ,且
,且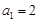 .
.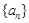 的通项公式;
的通项公式; 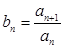 ,当数列
,当数列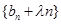 为递增数列时,求正实数
为递增数列时,求正实数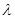 的取值范围.
的取值范围.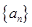 的前
的前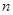 项和
项和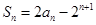 .
.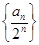 是等差数列;
是等差数列;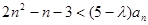 对
对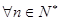 恒成立,求
恒成立,求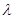 的取值范围.
的取值范围.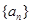 满足
满足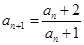 ,且
,且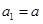 ,
,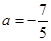 时,求出数列
时,求出数列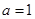 时,设
时,设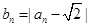 ,证明:
,证明: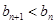 ;
;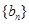 的前
的前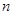 项和为
项和为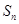 ,证明:
,证明: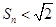 .
.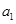 ,
,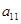 ,
,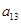 成等比数列.
成等比数列.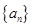 的通项公式;
的通项公式;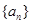 的首项
的首项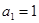 ,公差
,公差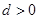 ,且第2项、第5项、第14项分别是等比数列
,且第2项、第5项、第14项分别是等比数列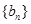 的第2项、第3项、第4项.
的第2项、第3项、第4项.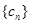 对任意的
对任意的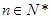 ,均有
,均有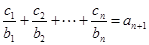 成立,求
成立,求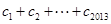 .
.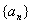 是各项都为正数的等比数列,
是各项都为正数的等比数列, 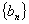 是等差数列,且
是等差数列,且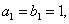 ,
,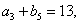
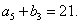
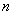 项和为
项和为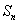 ,求证:
,求证: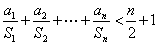 ;
;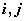 均为正整数,且
均为正整数,且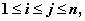 记所有可能乘积
记所有可能乘积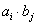 的和
的和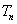 ,求证:
,求证: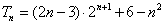 .
.