题目内容
7.在等腰直角△ABC中,$∠A=\frac{π}{2},AB=AC=1$,M是斜边BC上的点,满足$\overrightarrow{BC}=3\overrightarrow{BM}$(1)试用向量$\overrightarrow{AB},\overrightarrow{AC}$来表示向量$\overrightarrow{AM}$;
(2)若点P满足$|{\overrightarrow{AP}}|=1$,求$\overrightarrow{AP}•\overrightarrow{BM}$的取值范围.
分析 (1)由题意画出图形,直接利用向量加法的三角形法则得答案;
(2)设$<\overrightarrow{AP},\overrightarrow{BC}>=θ$,由题意求得$|\overrightarrow{BC}|$,然后直接展开向量数量积求得$\overrightarrow{AP}•\overrightarrow{BM}$的取值范围.
解答 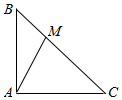 解:(1)如图,∵$\overrightarrow{BC}=3\overrightarrow{BM}$,
解:(1)如图,∵$\overrightarrow{BC}=3\overrightarrow{BM}$,
∴$\overrightarrow{AM}$=$\overrightarrow{AB}+\overrightarrow{BM}=\overrightarrow{AB}+\frac{1}{3}\overrightarrow{BC}=\overrightarrow{AB}+\frac{1}{3}(\overrightarrow{AC}-\overrightarrow{AB})$=$\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}$;
(2)设$<\overrightarrow{AP},\overrightarrow{BC}>=θ$,
∵$∠A=\frac{π}{2},AB=AC=1$,
∴$|\overrightarrow{BC}|=\sqrt{2}$,
则$\overrightarrow{AP}•\overrightarrow{BM}=\frac{1}{3}\overrightarrow{AP}•\overrightarrow{BC}=\frac{1}{3}|{\overrightarrow{AP}}|•|{\overrightarrow{BC}}|cosθ∈[{-\frac{{\sqrt{2}}}{3},\frac{{\sqrt{2}}}{3}}]$.
点评 本题考查平面向量的数量积运算,考查了向量的加法与减法的三角形法则,是中档题.

 星级口算天天练系列答案
星级口算天天练系列答案| A. | (-∞,2$\sqrt{2}$] | B. | (-∞,2$\sqrt{2}$) | C. | (-∞,3) | D. | (-∞,3] |
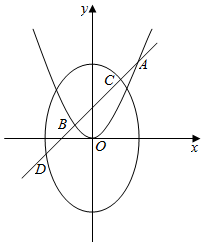 如图,抛物线C1:y=$\frac{1}{4}$x2的焦点F也是椭圆C2:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点,且在两曲线的一个公共点处的直线l1:$\sqrt{6}$x-2y-3=0与C1相切.
如图,抛物线C1:y=$\frac{1}{4}$x2的焦点F也是椭圆C2:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点,且在两曲线的一个公共点处的直线l1:$\sqrt{6}$x-2y-3=0与C1相切.