题目内容
已知 中,
中, ,
, ,则角
,则角 的取值范围是( )
的取值范围是( )
A. . . | B. | C. | D. |
C
解析试题分析:知道两边求角的范围,余弦定理得到角和第三边的关系,而第三边根据三角形的构成条件是有范围的,这样转化到角的范围.解:利用余弦定理得:4=c2+8-4 ccosA,即c2-4
ccosA,即c2-4 ccosA+4=0,,∴△=32cos2A-16≥0,∵A为锐角∴A∈
ccosA+4=0,,∴△=32cos2A-16≥0,∵A为锐角∴A∈ ,故选C
,故选C
考点:解三角形
点评:本题的考点是解三角形,主要考查利用余弦定理解答三角形有解问题,知道两边求角的范围,余弦定理得到角和第三边的关系,而第三边根据三角形的构成条件是有范围的,这样转化到角的范围,有一定难度

练习册系列答案
相关题目
在 中
中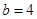 ,
,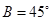 ,
,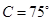 ,则
,则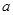 =( )
=( )
A.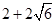 | B.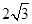 | C.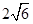 | D.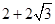 |
在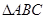 中,
中,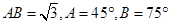 ,则BC =( )
,则BC =( )
A.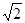 | B.2 | C.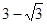 | D.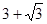 |
△ABC中,若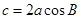 ,则△ABC的形状为( )
,则△ABC的形状为( )
| A.直角三角形 | B.等腰三角形 | C.等边三角形 | D.锐角三角形 |
在 中,若
中,若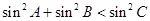 ,则
,则 的形状是( )
的形状是( )
| A.钝角三角形 | B.直角三角形 |
| C.锐角三角形 | D.不能确定 |
在△ABC中,若 ,则△ABC的形状是( )
,则△ABC的形状是( )
| A.直角三角形 | B.等边三角形 | C.等腰三角形 | D.不能确定 |
在△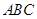 中,若
中,若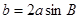 ,则
,则 等于( )
等于( )
A.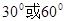 | B.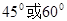 | C.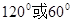 | D.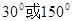 |
 的部分如图所示,点A、B是最高点,点C是最低点,若
的部分如图所示,点A、B是最高点,点C是最低点,若 是直角三角形,则
是直角三角形,则 的值为
的值为
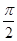 B.
B. C.
C. D.
D.
 ,
, , 则A=( )
, 则A=( )


