题目内容
△ABC中，若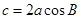
，则△ABC的形状为（ ）
| A．直角三角形 | B．等腰三角形 | C．等边三角形 | D．锐角三角形 |
B
解析试题分析：因为，△ABC中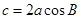， ，所以由余弦定理得，
，三角形为等腰三角形，故选B。
考点：正弦定理、余弦定理的应用。
点评：简单题，判定三角形的形状，一般有两种思路，一是转化成角的关系，二是转化成边的关系。
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
某人要制作一个三角形，要求它的三条高的长度分别是
，则此人 （ ）
| A．不能作出这样的三角形 | B．能作出一个锐角三角形 |
| C．能作出一个直角三角形 | D．能作出一个钝角三角形 |
飞机沿水平方向飞行，在A处测得正前下方地面目标C的俯角为30°，向前飞行10000米，到达B处，此时测得目标C的俯角为75°，这时飞机与地面目标的距离为
| A．5000米 | B．5000 米 | C．4000米 | D． 米 |
在△ABC中，若
，则角A＝（ ）
| A．30° | B．60° | C．120° | D．150° |
已知
中，
,
，则角
的取值范围是（ ）
A． . | B． | C． | D． |
在
中，如果有
，则的形状是（ ）
| A．等腰三角形或直角三角形 | B．直角三角形 |
| C．等腰直角三角形 | D．等边三角形 |
若△
的三个内角满足
，则△
| A．一定是锐角三角形 |
| B．一定是直角三角形 |
| C．一定是钝角三角形 |
| D．可能是锐角三角形，也可能是钝角三角形 |
在
中，已知
，则这个三角形解的情况是（ ）
| A．有一个解 | B．有两个解 | C．无解 | D．不能确定 |