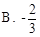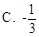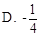题目内容
在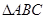 中,
中,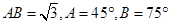 ,则BC =( )
,则BC =( )
A.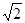 | B.2 | C.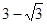 | D.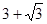 |
A
解析试题分析:因为,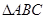 中,
中,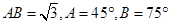 ,
,
所以,C=180°-(45°+75°)=60°,
由正弦定理, ,选A。
,选A。
考点:三角形内角和定理,正弦定理的应用。
点评:简单题,三角形中的问题,往往要用到三角形内角和定理,这是一个重要的“隐含条件”。

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
在△ABC中,∠A=60°,a= ,b=2,满足条件的△ABC( )
,b=2,满足条件的△ABC( )
| A.无解 | B.有解 | C.有两解 | D.有一解 |
设 的内角
的内角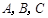 所对的边
所对的边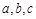 成等比数列,则
成等比数列,则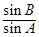 的取值范围是( )
的取值范围是( )
A.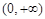 | B.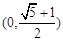 |
C.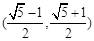 | D.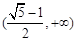 |
一艘轮船按北偏西 方向以每小时30海里的速度从
方向以每小时30海里的速度从 处开始航行,此时灯塔
处开始航行,此时灯塔 在轮船的北偏东45
在轮船的北偏东45 方向上,经过40分钟后轮船到达
方向上,经过40分钟后轮船到达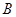 处,灯塔在轮船的东偏南15
处,灯塔在轮船的东偏南15 方向上,则灯塔
方向上,则灯塔 到轮船起始位置
到轮船起始位置 的距离是( )海里。
的距离是( )海里。
A.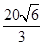 | B.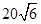 | C. | D. |
飞机沿水平方向飞行,在A处测得正前下方地面目标C的俯角为30°,向前飞行10000米,到达B处,此时测得目标C的俯角为75°,这时飞机与地面目标的距离为
| A.5000米 | B.5000 米 米 | C.4000米 | D. 米 米 |
在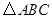 中,内角A,B,C的对边分别是
中,内角A,B,C的对边分别是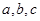 ,若
,若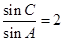 ,
,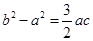 ,则
,则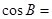 ( )
( )
A.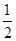 | B.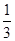 | C.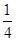 | D.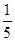 |
已知 中,
中, ,
, ,则角
,则角 的取值范围是( )
的取值范围是( )
A. . . | B. | C. | D. |
在△ABC中,已知a= ,b=2,B=45°,则角A=( ).
,b=2,B=45°,则角A=( ).
| A.30°或150° | B.60°或120° | C.60° | D.30° |
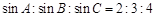 ,那么cosC等于 ( )
,那么cosC等于 ( )