题目内容
8.已知函数$f(x)=cos(2ωx-\frac{π}{3})-2{cos^2}$ωx+2的图象的对称中心到对称轴的最短距离为$\frac{π}{4}$.(1)求ω的值和函数f(x)的图象的对称中心、对称轴方程.
(2)求函数f(x)在区间$[{-\frac{π}{12},\frac{π}{2}}]$上的值域.
分析 (1)利用二倍角和两角和与差以及辅助角公式基本公式将函数化为y=Asin(ωx+φ)的形式,对称中心到对称轴的最短距离为$\frac{π}{4}$.可得周期T=π,根据周期公式求ω的值即可,根据正弦函数的性质求解对称中心、对称轴方程;
(2)x在区间$[{-\frac{π}{12},\frac{π}{2}}]$上时,求出内层函数的取值范围,结合三角函数的图象和性质,求出f(x)的取值最大和最小值,即得到f(x)的值域.
解答 解:(1)函数$f(x)=cos(2ωx-\frac{π}{3})-2{cos^2}$ωx+2
化简可得:$f(x)=\frac{1}{2}cos2ωx+\frac{{\sqrt{3}}}{2}sin2ωx-cos2ωx+1=sin(2ωx-\frac{π}{6})+1$,
∵对称中心到对称轴的最短距离为$\frac{π}{4}$.
∴周期π.
故得ω=1;
∴f(x)=sin(2x-$\frac{π}{6}$)+1.
由2x-$\frac{π}{6}$=$kπ+\frac{π}{2}$,(k∈Z)得:x=$\frac{1}{2}kπ+\frac{π}{3}$
∴函数图象的对称轴方程为x=$\frac{1}{2}kπ+\frac{π}{3}$(k∈Z)
函数的对称中心横坐标2x-$\frac{π}{6}$=kπ,(k∈Z),得x=$\frac{1}{2}kπ+\frac{π}{12}$
∴函数的对称中心坐标为$({\frac{kπ}{2}+\frac{π}{12},1})$(k∈Z)
(2)∵x∈$[{-\frac{π}{12},\frac{π}{2}}]$上时,
2x-$\frac{π}{6}$∈[$-\frac{π}{3}$,$\frac{5π}{6}$],
当2x-$\frac{π}{6}$=$-\frac{π}{3}$时,函数f(x)取得最小值为$-\frac{\sqrt{3}}{2}+1$.
当2x-$\frac{π}{6}$=$\frac{π}{2}$时,函数f(x)取得最大值为2.
∴函数f(x)在区间$[{-\frac{π}{12},\frac{π}{2}}]$上的值域为$[{-\frac{{\sqrt{3}}}{2}+1,2}]$.
点评 本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用,利用三角函数公式将函数进行化简是解决本题的关键.属于中档题.

 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案| A. | (¬p)∨(¬q) | B. | p∨(¬q) | C. | p∨q | D. | (¬p)∧(¬q) |
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 非奇非偶函数 | D. | 既是奇函数又是偶函数 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
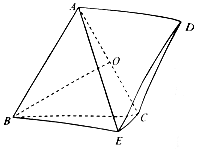 在多面体ABCDE中,平面ABC⊥平面BCE,四边形ABED为平行四边形,AB=AC=BC=2,CE=1,BE=$\sqrt{5}$,O为AC的中点.
在多面体ABCDE中,平面ABC⊥平面BCE,四边形ABED为平行四边形,AB=AC=BC=2,CE=1,BE=$\sqrt{5}$,O为AC的中点.