题目内容
10．已知偶函数f（x）=ax4+bx3+cx2+d的图象经过点（0，1），且在x=1处的切线方程是y=x-2，则y=f（x）的解析式为f（x）=$\frac{5}{2}$x4-$\frac{9}{2}$x2+1．分析 由题意可得d=1，由偶函数的性质可得b=0，求得函数的导数，求得切线的斜率和切点，由切线的方程可得a，c的方程，解方程可得a，c，进而得到所求解析式．
解答 解：由f（x）=ax4+bx3+cx2+d的图象经过点（0，1），
可得f（0）=1，即d=1，
由f（x）=ax4+bx3+cx2+d为偶函数，
可得b=0，
又f′（x）=4ax3+2cx，
即有在x=1处的切线斜率为4a+2c，
在x=1处的切线方程是y=x-2，
可得4a+2c=1，a+c+d=-1，
解得a=$\frac{5}{2}$，c=-$\frac{9}{2}$，
则f（x）=$\frac{5}{2}$x4-$\frac{9}{2}$x2+1．
故答案为：f（x）=$\frac{5}{2}$x4-$\frac{9}{2}$x2+1．
点评 本题考查导数的运用：求切线的斜率，考查函数的解析式的求法，注意运用偶函数的性质和待定系数法，考查运算能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
15．函数y=f（x）满足对任意x1，x2∈[0，2]（x1≠x2），$\frac{f（{x}_{2}）-f（{x}_{1}）}{{x}_{2}-{x}_{1}}$＞0，且函数f（x+2）是偶函数，则下列结论成立的是（ ）
| A． | f（1）＜f（$\frac{5}{2}$）＜f（$\frac{7}{2}$） | B． | f（$\frac{7}{2}$）＜f（1）＜f（$\frac{5}{2}$） | C． | f（$\frac{7}{2}$）＜f（$\frac{5}{2}$）＜f（1） | D． | f（$\frac{5}{2}$）＜f（1）＜f（$\frac{7}{2}$） |
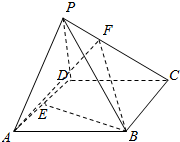如图所示，P为?ABCD所在平面外一点，E为AD的中点，F为PC上一点，当PA∥平面EBF时，$\frac{PF}{FC}$=$\frac{1}{2}$．