题目内容
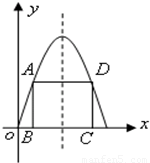
如图,在二次函数f(x)=4x-x2的图象与x轴所围成的图形中有一个内接矩形ABCD,求这个矩形的最大面积.
分析:本题考查常见函数的导数及用导数求最值等知识点.求函数最值的关键是选好自变量建立目标函数.一般说来,若f(x)是关于x的二次函数,可用配方法,也可用求导的方法求最值;若f(x)是三次或三次以上函数,则用求导的方法求最值,但均需注意函数的定义域.
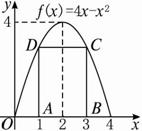
解:如上图,f(x)=4x-x2=-(x-2)2+4,它的对称轴方程是x=2,顶点坐标是(2,4).
不妨设A(x,0)(0<x<2),则B(4-x,0),D(x,f(x)).
∵D(x,f(x))在抛物线上,∴f(x)=4x-x2.
∴S矩形ABCD=(4-2x)(4x-x2)
=2x3-12x2+16x(0<x<2).
∴S′=6x2-24x+16.
令S′=0,得x1=2-![]() ,x2=2+
,x2=2+![]() (舍去).
(舍去).
又∵S矩形ABCD在x∈(0,2)上只有一个极值点,
∴它必是一个最值点.
∴[S矩形ABCD]max=2(2-![]() )3-12(2-
)3-12(2-![]() )2+16(2-
)2+16(2-![]() )=
)=![]() .
.

练习册系列答案
相关题目
 如图,在二次函数f(x)=4x-x2的图象与x轴所围成的图形中有一个内接矩形ABCD,设点B(x,0),则x=
如图,在二次函数f(x)=4x-x2的图象与x轴所围成的图形中有一个内接矩形ABCD,设点B(x,0),则x=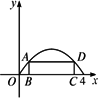
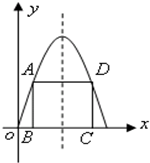 如图,在二次函数f(x)=4x-x2的图象与x轴所围成的图形中有一个内接矩形ABCD,设点B(x,0),则x=________,矩形面积最大.
如图,在二次函数f(x)=4x-x2的图象与x轴所围成的图形中有一个内接矩形ABCD,设点B(x,0),则x=________,矩形面积最大.