题目内容
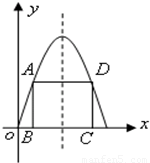
如图,在二次函数f(x)=4x-x2的图象与x轴所围成的图形中,有一矩形ABCD,求这个矩形ABCD的最大面积.
答案:
解析:
解析:
解:设点B的坐标为(x,0)(0<x<2),则矩形ABCD的面积S=(2-x)·2·(4x-x2)
=2(x3-6x2+8x).
∴![]() =2(3x2-12x+8).
=2(3x2-12x+8).
由![]() =0得x=
=0得x=![]() 或x=2+
或x=2+![]() (不合题意舍去),
(不合题意舍去),
当0<x<2-![]() 时,
时,![]() >0;
>0;
当2-![]() <x<2时,
<x<2时,![]() <0,
<0,
所以x=2-![]() 时,S有最大值
时,S有最大值![]() .
.

练习册系列答案
相关题目
 如图,在二次函数f(x)=4x-x2的图象与x轴所围成的图形中有一个内接矩形ABCD,设点B(x,0),则x=
如图,在二次函数f(x)=4x-x2的图象与x轴所围成的图形中有一个内接矩形ABCD,设点B(x,0),则x=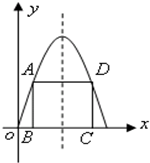 如图,在二次函数f(x)=4x-x2的图象与x轴所围成的图形中有一个内接矩形ABCD,设点B(x,0),则x=________,矩形面积最大.
如图,在二次函数f(x)=4x-x2的图象与x轴所围成的图形中有一个内接矩形ABCD,设点B(x,0),则x=________,矩形面积最大.