题目内容
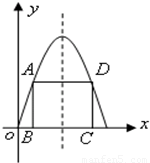
 如图,在二次函数f(x)=4x-x2的图象与x轴所围成的图形中有一个内接矩形ABCD,设点B(x,0),则x=
如图,在二次函数f(x)=4x-x2的图象与x轴所围成的图形中有一个内接矩形ABCD,设点B(x,0),则x=2-
2
| ||
| 3 |
2-
,矩形面积最大.2
| ||
| 3 |
分析:先求出矩形的长和宽,然后表示出其面积,最后利用导数研究函数的值域即可.
解答:解:根据点B(x,0)则A(x,4x-x2),C(4-x,0)
∴矩形面积S=(4-2x)(4x-x2)其中(0<x<4)
S=2x3-12x2+16x (0<x<4)
S′=6x2-24x+16=0解得x=2-
或2+
根据题意可知当x=2-
时矩形面积最大.
故答案为:2-
∴矩形面积S=(4-2x)(4x-x2)其中(0<x<4)
S=2x3-12x2+16x (0<x<4)
S′=6x2-24x+16=0解得x=2-
2
| ||
| 3 |
2
| ||
| 3 |
根据题意可知当x=2-
2
| ||
| 3 |
故答案为:2-
2
| ||
| 3 |
点评:本题主要考查了二次函数的性质和三次函数的最大值,同时考查了利用导数研究函数的最值,属于基础题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
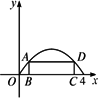
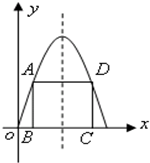 如图,在二次函数f(x)=4x-x2的图象与x轴所围成的图形中有一个内接矩形ABCD,设点B(x,0),则x=________,矩形面积最大.
如图,在二次函数f(x)=4x-x2的图象与x轴所围成的图形中有一个内接矩形ABCD,设点B(x,0),则x=________,矩形面积最大.