题目内容
3.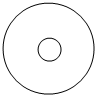 某家庭游戏中有这样一个“投币”活动,活动道具是如图所示的半径为10cm的圆形纸板,纸板上有一个相同圆心、半径为2cm的小圆,现让家庭中的每名成员向此纸板抛掷一枚半径为1cm的硬币,使硬币整体随机落在纸板内,若硬币落下后与小圆圆面(不包含边界)无公共点则中奖,否则不中奖.
某家庭游戏中有这样一个“投币”活动,活动道具是如图所示的半径为10cm的圆形纸板,纸板上有一个相同圆心、半径为2cm的小圆,现让家庭中的每名成员向此纸板抛掷一枚半径为1cm的硬币,使硬币整体随机落在纸板内,若硬币落下后与小圆圆面(不包含边界)无公共点则中奖,否则不中奖.(1)求中奖的概率;
(2)若某家庭中有3名成员参与“投币”活动,记这3名成员中中奖的人数为E,求E的分布列和数学期望.
分析 (1)由题意可得,硬币要落在纸板内,硬币圆心距离纸板圆心的距离应该小于9.硬币与小圆无公共点,硬币圆心距离小圆圆心要大于2,先求出硬币落在纸板上的面积,然后再求解硬币落下后与小圆没交点的区域的面积,代入古典概率的计算公式可求中奖的概率.
(2)由题意E~B(3,$\frac{8}{9}$),由此能求出E的分布列和数学期望.
解答 解:(1)记“中奖”为事件A
硬币要落在纸板内,硬币圆心距离纸板圆心的距离应该小于9,其面积为81π
无公共点也就意味着,硬币的圆心与纸板的圆心相距超过3cm
以纸板的圆心为圆心,作一个半径3cm的圆,硬币的圆心在此圆外面,则硬币与半径为2cm的小圆无公共点,此半径为3的圆面积是9π
所以有公共点的概率为$\frac{9π}{81π}$=$\frac{1}{9}$,
中奖的概率P(A)=1-$\frac{1}{9}$=$\frac{8}{9}$.
(2)由题意E~B(3,$\frac{8}{9}$),
P(E=0)=${C}_{3}^{0}(\frac{1}{9})^{3}$=$\frac{1}{729}$,
P(E=1)=${C}_{3}^{1}(\frac{8}{9})(\frac{1}{9})^{2}$=$\frac{24}{729}$,
P(E=2)=${C}_{3}^{2}(\frac{8}{9})^{2}(\frac{1}{9})$=$\frac{192}{729}$,
P(E=3)=${C}_{3}^{3}(\frac{8}{9})^{3}$=$\frac{512}{729}$,
∴E的分布列为:
| E | 0 | 1 | 2 | 3 |
| P | $\frac{1}{729}$ | $\frac{24}{729}$ | $\frac{192}{729}$ | $\frac{512}{729}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意二项分布的性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.已知复数z满足(z-i)i=2+3i,则|z|=( )
| A. | $\sqrt{10}$ | B. | 3$\sqrt{2}$ | C. | 10 | D. | 18 |
14.在△ABC中,角C,B所对的边长为c,b,则“c=b”是“ccosC=bcosB”的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分又不必要 |
11.设i是虚数单位,则复数z=($\frac{1}{2}$-$\frac{\sqrt{3}}{2}$i)2的共轭复数$\overline{z}$=( )
| A. | -$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i | B. | -$\frac{1}{2}$-$\frac{\sqrt{3}}{2}$i | C. | $\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i | D. | $\frac{1}{2}$-$\frac{\sqrt{3}}{2}$i |
15.计算[(-$\sqrt{2}$)2]-$\frac{1}{2}$的结果是( )
| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |