题目内容
把正奇数1,3，5,7，…顺次分组，组成一个新的数列:a1=1,a2=3+5,a3=7+9+11,…,其中an是n个奇数的和.?(1)求an；?
(2)求Sn=a1+a2+…+an.
解析:(1)由题意知，数列｛an｝中，前n-1项共有1+2+…+(n-1)=
项.?
又由于原数列为奇数列{2n-1},?
∴an-1中最后一个数是2［
］-1=n2-n-1.?
∴an中最前面的一个数是(n2-n-1)+2=n2-n+1.?
∴an=n(n2-n+1)+ 
·2=n3.??
(2)Sn=13+23+…+n3,?
Sn中共有1＋2＋…＋n=
项为奇数，?
∴Sn=1+(3+5)+(7+9+11)+…?
=1·
.
练习册系列答案
相关题目
中的数按上小下大、左小右大的原则排成如下三角形数表：
是位于这个三角形数表中从上往下数第
行、从左往右数第
个数．
，求
的值；
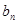，求证
．（本题满分14分）
中的数按上小下大、左小右大的原则排成如下三角形数表： 
是位于这个三角形数表中从上往下数第
行、从左往右数第
个数
，求
的值；
，若记三角形数表中从上往下数第n行各数的和为
，求数列
的前n项和
。
)n·
(x＞0)，若记三角形数表中从上往下数第n行各数的和为bn，求数列{f(bn)}的前n项和Sn.