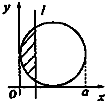题目内容
5.已知△ABC的顶点坐标是A(-1,5)、B(-2,-1)、C(4、7),求BC边上中线所在的直线方程和BC的长.分析 求出BC的中点坐标,用两点式写出直线方程,再化为一般方程;利用两点的距离公式计算|BC|.
解答 解:∵△ABC的顶点坐标是A(-1,5)、B(-2,-1)、C(4、7),
∴BC的中点为M(1,3),
∴BC边上中线所在的直线方程为:$\frac{y-3}{5-3}$=$\frac{x-1}{-1-1}$,
化为一般方程是x+y-4=0;
BC的长为|BC|=$\sqrt{{(4+2)}^{2}{+(7+1)}^{2}}$=10.
点评 本题考查了直线方程的应用问题,也考查了求平面上两点间的距离的应用问题,是基础题目.

练习册系列答案
相关题目
3.执行如图的程序框图,若输出的k=2,则输入x的取值范围是( )
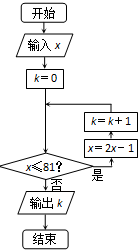

| A. | (21,41) | B. | [21,41] | C. | (21,41] | D. | [21,41) |
15.A和B是抛物线y2=8x上除去原点以外的两个动点,O是坐标原点且满足$\overrightarrow{OA}•\overrightarrow{OB}$=0,$\overrightarrow{OM}•\overrightarrow{AB}$=0,则支动点M的轨迹方程为( )
| A. | x2+y2-8x=0 | B. | y=6x2 | C. | x2+4y2=1 | D. | $\frac{x^2}{9}-\frac{y^2}{4}$=1 |
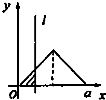
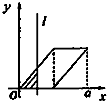
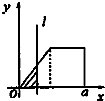
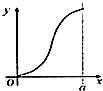 如图,有四个平面图形分别是三角形、平行四边形、直角梯形、圆.垂直于x轴的直线l:x=t(0≤t≤a)经过原点O向右平行移动,l在移动过程中扫过平面图形的面积为y(图中阴影部分),若函数y=f(t)的大致图象如图,那么平面图形的形状不可能是( )
如图,有四个平面图形分别是三角形、平行四边形、直角梯形、圆.垂直于x轴的直线l:x=t(0≤t≤a)经过原点O向右平行移动,l在移动过程中扫过平面图形的面积为y(图中阴影部分),若函数y=f(t)的大致图象如图,那么平面图形的形状不可能是( )