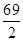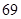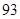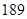题目内容
设等比数列{an}的前n项和为Sn.已知an+1=2Sn+2(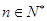 )
)
(1)求数列{an}的通项公式;
(2)在an与an+1之间插入n个数,使这n+2个数组成一个公差为dn的等差数列,
①在数列{dn}中是否存在三项dm,dk,dp(其中m,k,p成等差数列)成等比数列?若存在,求出这样的三项,若不存在,说明理由;
②求证: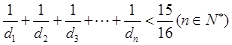 .
.
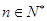 )
)(1)求数列{an}的通项公式;
(2)在an与an+1之间插入n个数,使这n+2个数组成一个公差为dn的等差数列,
①在数列{dn}中是否存在三项dm,dk,dp(其中m,k,p成等差数列)成等比数列?若存在,求出这样的三项,若不存在,说明理由;
②求证:
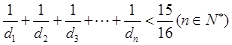 .
.(1)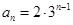 (2)见解析
(2)见解析
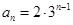 (2)见解析
(2)见解析试题分析:
(1)利用Sn与an之间的关系
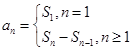 ,即可得到关于an+1,an的递推式,证明an为等比数列,且可以知道公比,当n=1时,可以得到a1与a2之间的关系,在根据an等比数列,可以消掉a2得到首项的值,进而得到通项公式.
,即可得到关于an+1,an的递推式,证明an为等比数列,且可以知道公比,当n=1时,可以得到a1与a2之间的关系,在根据an等比数列,可以消掉a2得到首项的值,进而得到通项公式.(2)根据等差数列公差与项之间的关系(
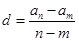 ),可以得到
),可以得到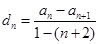 ,带入an得到dn的通项公式.
,带入an得到dn的通项公式.①假设存在,dm,dk,dp成等比数列,可以得到关于他们的等比中项式子,把dn的通项公式带入计算可以得到
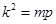 ,则m,k,p既成等差数列也是等比数列,所以三者相等,与数列{dn}中是否存在三项dm,dk,dp(不相等)矛盾,所以是不存在的.
,则m,k,p既成等差数列也是等比数列,所以三者相等,与数列{dn}中是否存在三项dm,dk,dp(不相等)矛盾,所以是不存在的.②利用(2)所得求出
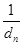 的通项公式,再利用错位相减可以求得
的通项公式,再利用错位相减可以求得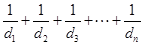 ,利用不等式的性质即可得到
,利用不等式的性质即可得到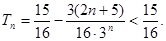 证明原式.
证明原式.试题解析:
(1)由
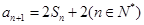 ,
,可得:
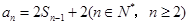 ,
,两式相减:
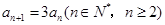 . 2分
. 2分又
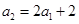 ,
,因为数列
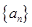 是等比数列,所以
是等比数列,所以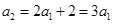 ,故
,故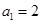 .
.所以
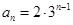 . 4分
. 4分(2)由(1)可知
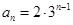 ,
,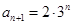
因为:
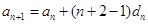 ,故:
,故: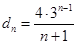 . 6分
. 6分①假设在数列
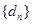 中存在三项
中存在三项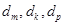 (其中
(其中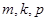 成等差数列)成等比数列,
成等差数列)成等比数列,则:
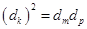 ,即:
,即: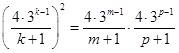 ,
,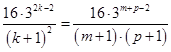 (*) 8分
(*) 8分因为
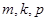 成等差数列,所以
成等差数列,所以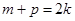 ,
,(*)可以化简为
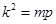 ,故
,故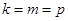 ,这与题设矛盾.
,这与题设矛盾.所以在数列
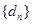 中不存在三项
中不存在三项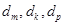 (其中
(其中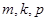 成等差数列)成等比数列.10分
成等差数列)成等比数列.10分②令
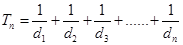 ,
,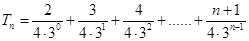 ,
,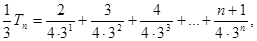 11分
11分两式相减:
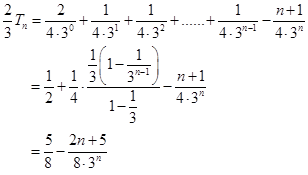 13分
13分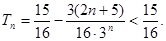 . 14分
. 14分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的前
的前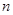 项和为
项和为 ,且对任意正整数
,且对任意正整数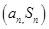 都在直线
都在直线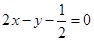 上.求数列
上.求数列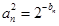 设
设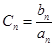 求:数列
求:数列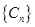 前
前 .
.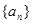 的前
的前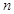 项和为
项和为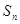 ,对一切正整数
,对一切正整数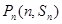 都在函数
都在函数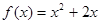 的图象上.
的图象上.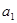 ,
,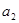 ;
;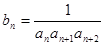 ,求证数列
,求证数列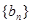 的前
的前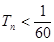 .
.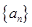 的前
的前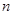 项和为
项和为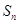 ,且
,且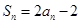 ,
,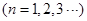 ;数列
;数列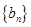 中,
中,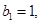 点
点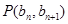 在直线
在直线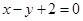 上.
上.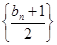 的前
的前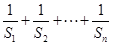 ;
;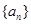 的通项公式为
的通项公式为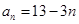 ,
,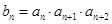 ,
,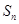 是数列
是数列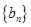 的前
的前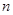 项和,则
项和,则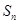 的最大值为( )
的最大值为( )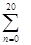 (1+2n)=________.
(1+2n)=________.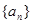 的前
的前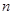 项和为
项和为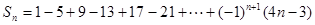 ,则
,则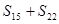 的值是( )
的值是( )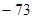
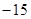
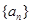 是由正数组成的等比数列,
是由正数组成的等比数列,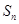 表示
表示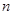 项的和,若
项的和,若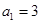 ,
,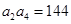 ,则
,则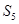 的值是 ( )
的值是 ( )