Question

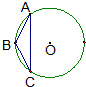
在极坐标系中，定点A（1，），动点B在直线ρcosθ+ρsinθ=0上运动，当线段AB最短时，动点B的极坐标是

1. A.
   （，）
2. B.
   （，）
3. C.
   （，）
4. D.
   （，）

Answer 1

B
分析：将直线ρcosθ+ρsinθ=0化为一般方程，再利用线段AB最短可知直线AB与已知直线垂直，设出直线AB的方程，联立方程求出B的坐标，从而求解．
解答：∵x=ρcosθ，y=ρsinθ，代入直线ρcosθ+ρsinθ=0，
可得x+y=0…①，
∵定点A（1，），与动点B在直线ρcosθ+ρsinθ=0上运动，当线段AB最短时，此时直线AB垂直于直线x+y=0，
设直线AB为：y-=1×（x-1），即y=x-1+…②，
联立方程①②求得交点B（-，-），
∴B极坐标为ρ==，tanθ==-1，∴θ=-．
故选B．
点评：此题主要考查极坐标与一般方程之间的转化，是一道基础题，注意极坐标与一般方程的关系：ρ=，tanθ=，x=ρcosθ，y=ρsinθ．