Question

（2011•浦东新区三模）在极坐标系中，定点A(1，

π

2

)，动点B在曲线ρ=2cosθ上移动，当线段AB最短时，点B的极径为

2- 2

．

Answer 1

分析：在极坐标系中，如图，线段AB最短，B就是过A与圆心的直线，和圆的交点．再利用余弦定理即可求得点B的极径OB的长即可．

解答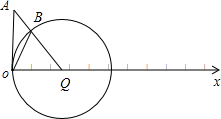：解：在极坐标系中，定点A(1，

π

2

)，曲线ρ=2cosθ表示圆心在Q（1，0），半径为1的圆，如图．
线段AB最短，B就是过A与圆心的直线和圆的交点，
在三角形OBQ中，由余弦定理得：
OB²=OQ²+QB²-2OQ•QBcos∠OQB=2-

2

，
所以点B的极径为

2- 2

故答案为：

2- 2

．

点评：此题主要考查极坐标与一般方程之间的转化，是一道基础题，注意极坐标与一般方程的关系：ρ=

x2+y2

，tanθ=

y

x

，x=ρcosθ，y=ρsinθ．