题目内容

在极坐标系中，定点A(1，
π2
)，点B在直线ρcosθ+ρsinθ=0上运动，当线段AB最短时，点B的极坐标是
 
．
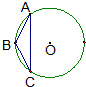
分析：在极坐标系中，直线ρcosθ+ρsinθ=0，化为x+y=0，线段AB最短，就是过A与x+y=0垂直的直线，和它的交点．再换成极坐标．
解答：解：直线ρcosθ+ρsinθ=0，化为x+y=0，与x+y=0垂直过A的直线方程为：y-1=x，这两条直线的交点是(-
1
2
，
1
2
)．
所以B的极坐标是(
2
2
，
3π
4
)．
故答案为：(
2
2
，
3π
4
)．
点评：本题是极坐标和直角坐标方程，极坐标和直角坐标的互化，容易出错．
练习册系列答案
相关题目
（坐标系与参数方程选做题）在极坐标系中，定点A（2，π），动点B在直线ρsin(θ+
π
4
)=
2
2
上运动，则线段AB的最精英家教网短长度为
 

（不等式选讲选做题）设函数f（x）=|x-1|+|x-2|，则f（x）的最小值为
 

（几何证明选讲选做题） 如图所示，等腰三角形ABC的底边AC长为6，其外接圆的半径长为5，则三角形ABC的面积是
 
．
在极坐标系中，定点A（1，
π
2
），动点B在直线ρcosθ+ρsinθ=0上运动，当线段AB最短时，动点B的极坐标是（　　）
A、（
2
2
，
π
4
）
B、（
2
2
，
3π
4
）
C、（
3
2
，
π
4
）
D、（
3
2
，
3π
4
）
（2011•浦东新区三模）在极坐标系中，定点A(1，
π
2
)，动点B在曲线ρ=2cosθ上移动，当线段AB最短时，点B的极径为
2-
2
2-
2
．
（2013•广州一模）（坐标系与参数方程选讲选做题）
在极坐标系中，定点A(2，
3
2
π)，点B在直线ρcosθ+
3
ρsinθ=0上运动，当线段AB最短时，点B的极坐标为
(1，
11π
6
)
(1，
11π
6
)
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网