题目内容
1.若函数y=3+ax-1的图象恒过P点,则P点坐标是( )| A. | (2,3) | B. | (4,1) | C. | (3,2) | D. | (1,4) |
分析 由指数函数的图象恒过(0,1),然后结合函数图象的平移变换得答案.
解答 解:∵y=ax恒过定点(0,1),且y=3+ax-1是把y=ax的图象向右平移1个单位,再向上平移3个单位得到的,
∴函数y=3+ax-1的图象恒过P(1,4),
故选:D.
点评 本题考查指数函数的图象变换,考查了指数函数的性质,是基础题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
9.过点M(1,4)与两条坐标轴围成的三角形面积等于1的所在直线方程是( )
| A. | 2x-y+2=0 | B. | 3x-y+1=0 | ||
| C. | 8x-y-4=0 | D. | 2x-y+2=0或8x-y-4=0 |
16.已知p:函数y=2|x-1|的图象关于直线x=1对称;q:函数y=x+$\frac{1}{x}$在(0,+∞)上是增函数,由它们组成的新命题“p∧q”“p∨q”“¬p”中,真命题的个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
13.若点A(-1,-1),B(1,3),C(x,5)三点共线,则使$\overrightarrow{AB}$=$λ\overrightarrow{BC}$成立的实数λ的值为( )
| A. | -2 | B. | 0 | C. | 1 | D. | 2 |
11.若-$\frac{3π}{4}$<α<-$\frac{π}{2}$,则sinα,cosα,tanα的大小关系是( )
| A. | sinα<tanα<cosα | B. | tanα<sinα<cosα | C. | cosα<sinα<tanα | D. | sinα<cosα<tanα |
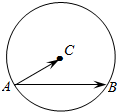 如图,定圆C的半径为4,A为圆C上的一个定点,B为圆C上的动点,若点A,B,C不共线,且$|{\overrightarrow{AB}-t\overrightarrow{AC}}|≥|{\overrightarrow{BC}}|$对任意的t∈(0,+∞)恒成立,则$\overrightarrow{AB}•\overrightarrow{AC}$=16.
如图,定圆C的半径为4,A为圆C上的一个定点,B为圆C上的动点,若点A,B,C不共线,且$|{\overrightarrow{AB}-t\overrightarrow{AC}}|≥|{\overrightarrow{BC}}|$对任意的t∈(0,+∞)恒成立,则$\overrightarrow{AB}•\overrightarrow{AC}$=16. 我校在高三某班参加夏令营的12名同学中,随机抽取6名,统计他们在参加夏令营期间完成测试项目的个数,并制成茎叶图如图所示,其中茎为十位数,叶为个位数
我校在高三某班参加夏令营的12名同学中,随机抽取6名,统计他们在参加夏令营期间完成测试项目的个数,并制成茎叶图如图所示,其中茎为十位数,叶为个位数