Question

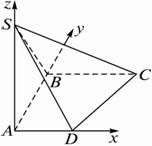
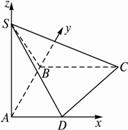
如图，ABCD是直角梯形，∠ABC=90°，SA⊥面ABCD，SA=AB=BC=1，AD=,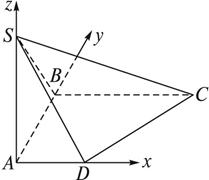

(1)求面SCD与面SBA所成的二面角的正切值；

(2)求SC与平面ABCD所成的角的正弦值.

Answer 1

解：(1)因为AD、AB、AS是三条两两互相垂直的线段，故以A为原点，以AD、AB、AS的方向为x轴、y轴、z轴的正方向建立坐标系，则A(0,0,0)、D(,0,0)、C(1,1,0)、S(0,0,1),=(,0,0)是平面SAB的法向量.设面SCD的法向量n=(1，λ，μ),则n·=(1，λ，μ)·(,1,0)=+λ=0,∴λ=-.

n·=(1,λ,μ)·(-,0,1)=-+μ=0,

∴μ=.

∴n=(1,-,).

如以θ表示欲求的二面角，则cos〈,n〉,

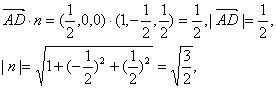
∴cosθ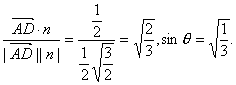

∴tanθ=

∴面SCD与面SBA所成二面角的正切值为

(2)∵是平面ABCD的法向量，先求与之间的夹角φ.

∵

∴

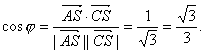∴又∵该夹角与直线SC与平面ABCD所成的角互余,

∴所求正弦值为.