Question

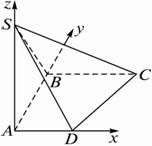
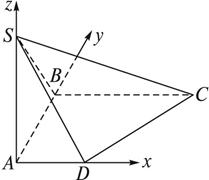
如图，ABCD是直角梯形，∠ABC=90°，SA⊥面ABCD?，SA=AB=BC=1，AD=.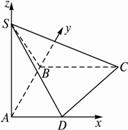

(1)求面SCD与面SBA所成的二面角的正切值；

(2)求SC与平面ABCD所成的角的余弦值.

Answer 1

解：(1)因为AD、AB、AS是三条两两互相垂直的线段，故以A为原点，以、、的方向为x轴、y轴、z轴的正方向建立坐标系，则A(0,0,0)、D(,0,0)、C(1,1,0)、S(0,0,1), =(,0,0)是平面SAB的法向量.设面SCD的法向量n=(1，λ，μ),则n=(1，λ，μ)  (,1,0)=+λ=0,∴λ=-.?

n=(1,λ,μ)  (- ,0,1)=- +μ=0,

∴μ=.

∴n=(1,-, ).?

如以θ表示欲求二面角的值，则cosθ=cos〈,n〉,?

n=(,0,0)  (1,- ,)=,||=,

n==,?

∴cosθ===,sinθ=.?

∴tanθ===.?

∴面SCD与面SBA所成二面角的正切值为.?

(2)∵是平面ABCD的法向量，先求与之间的夹角φ.?

∵=++,?

∴= (++)==1,?

||=1,?

||===,?

∴cosφ===.

∴所求余弦值为.

点评：对于(2)也可借助坐标计算线面角.像棱没有给出的二面角大小计算问题，用向量法解答十分方便.