Question

如图,四边形ABCD是直角梯形,AB∥CD,∠ADC=∠DAB=90°,CD=2AB,

PA⊥平面ABCD,PA=AB=AD,Q是PC的中点.

(1)求证:BQ∥平面PAD;

(2)探究在过BQ且与底面ABCD相交的平面中是否存在一个平面α,把四棱锥P—ABCD截成两部分,使得其中一部分为一个四个面都是直角三角形的四面体.若存在,求平面PBC与平面α所成锐二面角的余弦值;若不存在,请说明理由.

Answer 1

解:(1)取PD的中点F,连结AF、FQ,

∵Q为PC的中点,则FQ为△PCD的中位线,

∴FQ∥CD且FQ=CD.

又∵AB∥CD且AB=CD,

∴FQ∥AB且FQ=AB.

∴四边形ABQF为平行四边形,BQ∥AF.

又∵AF在平面PAD内,BQ在平面PAD外,

∴BQ∥平面PAD.

(2)设过BQ的平面与平面PCD交于QE,E为△PCD的边与平面α的交点,

当E为CD中点时,四面体Q—BCE的四个面都是直角三角形,证明如下:

∵当E为CD的中点时,则DE∥AB且DE=AB,∴四边形ABED为平行四边形.

∴BE∥AD.又∠ADC=90°,∴∠BEC=90°.故△BEC为直角三角形.

∵在△PAD中,AD=AP,F为PD的中点,

∴AF⊥PD.

又∵PA⊥平面ABCD,CD在平面ABCD内,

∴PA⊥CD.

又CD⊥AD,∴CD⊥面PAD.

∴∠FDC=90°.

又QE∥PD,∴∠CEQ=90°.

∴△CEQ为直角三角形.

又∵AF面PAD,∴AF⊥CD.

又PD∩CD=D,∴AF⊥面PCD.

由BQ∥AF得BQ⊥面PCD,由CQ,EQ都在平面PCD内,

∴BQ⊥CQ,BQ⊥EQ.

∴四面体Q—BCE的四个面都为直角三角形.

下面求平面PBC与平面α所有锐二面角的余弦值.

解法一:由上面求解过程知,BQ⊥面PCD,BQ⊥QE,BQ⊥QC,

∴∠EQC是截面α与平面QBC二面角的平面角.

设PA=AB=AD=1,则PD=,QE=,PC=,CQ=.

在Rt△QEC中,cos∠EQC===.

∴所求角的余弦值为.

解法二:坐标法  如图建立直角坐标系,

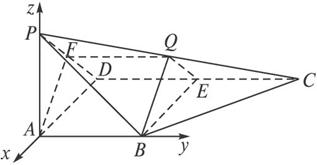
设PA=AB=AD=1,则A(0,0,0),B(0,1,0),C(-1,2,0),P(0,0,1).

则PB=(0,1,-1),BC=(-1,1,0),平面BQE的法向量为AB=(0,1,0).

设平面PBC的法向量为n=(x,y,z),

则n⊥PB,n⊥BC.由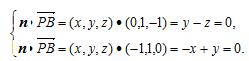

令x=1得n=(1,1,1).∴cos〈,n〉=.∴所求角的余弦值为.