题目内容
如图5，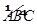
是半径为a的半圆，AC为直径，点E为
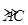的中点，点B和点C为线段AD的三等分点．平面AEC外一点F满足
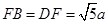，FE=
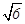a
．
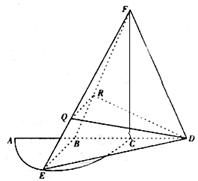
图5
（1）证明：EB⊥FD；
（2）已知点Q,R分别为线段FE,FB上的点，使得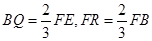
,求平面
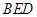与平面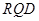
所成二面角的正弦值
【答案】
【解析】
（2）设平面
与平面RQD的交线为
.
由BQ=
FE,FR=FB知, 
.
而
平面
，∴
平面，
而平面
平面
= ，
∴
.
由（1）知，
平面，∴平面，
而
平面， 
平面，
∴
，
∴
是平面与平面所成二面角的平面角．
在
中，
，
，
．
．
故平面与平面所成二面角的正弦值是．
练习册系列答案
相关题目
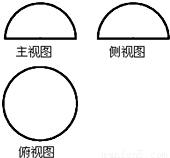
如右图是某几何体的三视图，其中主视图和侧视图是半径为1的半圆，俯视图是个圆，则该几何体的全面积是（ ）| A、2π | B、3π | C、4π | D、5π |
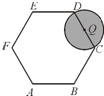如图，在边长为2的正六边形ABCDEF中，动圆Q的半径为1，圆心在线段CD（含端点）上运动，P是圆Q上及内部的动点，设向量| AP |
| AB |
| AF |
| A、（1，2] |
| B、[5，6] |
| C、[2，5] |
| D、[3，5] |
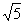a，FE=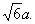
，
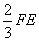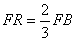,求平面BED与平面RQD所成二面角的正弦值.