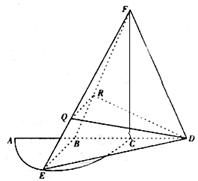
题目内容
|
|||
|
|||
|
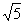 a,FE=
a,FE=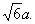
(1)证明:EB⊥FD;
(2)已知点Q,R分别为线段FE,FB上的点,使得BQ=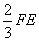 ,
,
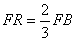 ,求平面BED与平面RQD所成二面角的正弦值.
,求平面BED与平面RQD所成二面角的正弦值.
【答案】

证明:(1)连结CF。
因为△AEC是半径为a的半圆,AC为直径,点E为AC的中点,
所以


所以△BDF是等腰三角形,且点C是底边BD的中点,所以CF⊥BD,


即
|



(2)设平面 与平面RQD的交线为
与平面RQD的交线为 .
.
由BQ= FE,FR=
FE,FR= FB知,
FB知,  .
.
而 平面
平面 ,∴
,∴ 平面
平面 ,
,
而平面
 平面
平面 =
=  ,
,
∴ .
.
由(1)知,
 平面
平面 ,∴
,∴
 平面
平面 ,
,
而 平面
平面 ,
,
 平面
平面 ,
,
∴ ,
,
∴ 是平面
是平面 与平面
与平面 所成二面角的平面角.
所成二面角的平面角.
在 中,
中, ,
,
 ,
, .
.

由正弦定理知,


由正弦定理知,

 .
.
故平面 与平面
与平面 所成二面角的正弦值是
所成二面角的正弦值是 .
.

练习册系列答案
相关题目



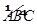 是半径为a的半圆,AC为直径,点E为
是半径为a的半圆,AC为直径,点E为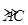 的中点,点B和点C为线段AD的三等分点.平面AEC外一点F满足
的中点,点B和点C为线段AD的三等分点.平面AEC外一点F满足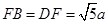 ,FE=
,FE=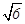 a
.
a
.
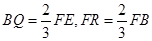 ,求平面
,求平面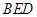 与平面
与平面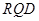 所成二面角的正弦值
所成二面角的正弦值