题目内容
若函数f（x）=（x+1）•（x-a）为偶函数，则实数a=________．
1
分析：根据偶函数f（x）的定义域为R，则?x∈R，都有f（-x）=f（x），建立等式，解之即可．
解答：因为函数f（x）=（x+1）•（x-a）是偶函数，
所以?x∈R，都有f（-x）=f（x）．
所以?x∈R，都有（-x+1）•（-x-a）=（x+1）•（x-a）
即x2+（a-1）x-a=x2-（a-1）x-a
所以a=1．
故答案为：1
点评：本题主要考查了函数奇偶性的性质，同时考查了运算求解的能力，属于基础题．
分析：根据偶函数f（x）的定义域为R，则?x∈R，都有f（-x）=f（x），建立等式，解之即可．
解答：因为函数f（x）=（x+1）•（x-a）是偶函数，
所以?x∈R，都有f（-x）=f（x）．
所以?x∈R，都有（-x+1）•（-x-a）=（x+1）•（x-a）
即x2+（a-1）x-a=x2-（a-1）x-a
所以a=1．
故答案为：1
点评：本题主要考查了函数奇偶性的性质，同时考查了运算求解的能力，属于基础题．
练习册系列答案
相关题目
若函数 f（x）＝a x (a＞0，a≠1 ) 的部分对应值如表：
| x | －2 | 0 |
| f（x） | 0.592 | 1 |
则不等 式f－1（│x│＜0）的解集是 （）
A. {x│－1＜x＜1} B. {x│x＜－1或x＞1}
C. {x│0＜x＜1} D. {x│－1＜x＜0或0＜x＜1}
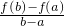（x-a）|≤T（T为常数）成立，则称函数f（x）在[a，b]上具有“T级线性逼近”．下列函数中：
；
级线性逼近”的函数的个数为
（x-a）|≤T（T为常数）成立，则称函数f（x）在[a，b]上具有“T级线性逼近”．下列函数中：
；
级线性逼近”的函数的个数为（ ）