题目内容
扇形OAB的圆心角∠AOB=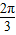 ,点P在圆弧AB上运动,且满足
,点P在圆弧AB上运动,且满足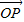 =x
=x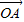 +y
+y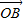 ,则x+y的取值范围为 .
,则x+y的取值范围为 .
【答案】分析: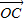 与
与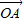 夹角为θ(0≤θ≤
夹角为θ(0≤θ≤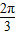 ),设
),设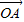 为直角坐标系的x轴,求出三个向量坐标,进而利用同角三角函数的平方关系,可得到x+y=2sin(θ+
为直角坐标系的x轴,求出三个向量坐标,进而利用同角三角函数的平方关系,可得到x+y=2sin(θ+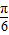 ),结合三角函数的图象和性质,可得答案.
),结合三角函数的图象和性质,可得答案.
解答: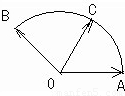 解:记
解:记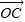 与
与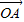 夹角为θ(0≤θ≤
夹角为θ(0≤θ≤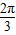 ),设
),设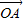 为直角坐标系的x轴.
为直角坐标系的x轴.
则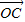 =(cosθ,sinθ),
=(cosθ,sinθ),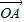 =(1,0),
=(1,0),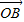 =(-
=(- ,
,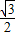 )
)
代入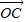 =x
=x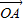 +y
+y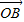 ,有(cos θ,sin θ)=(x,0)+(-
,有(cos θ,sin θ)=(x,0)+(-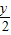 ,
,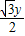 )
)
联立方程组:x-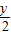 =cosθ,
=cosθ,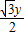 =sin θ
=sin θ
故x+y=2sin(θ+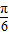 )
)
∵0≤θ≤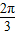 ,
,
∴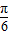 ≤θ+
≤θ+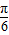 ≤
≤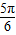
当θ+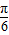 =
=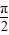 ,即θ=
,即θ=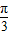 时,x+y取最大值2
时,x+y取最大值2
当θ+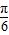 =
=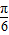 或
或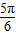 ,即θ=0<或
,即θ=0<或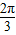 时,x+y取最小值1
时,x+y取最小值1
故答案为:[1,2]
点评:本题考查的知识点是平面向量的基本定理及其意义,其中建立坐标系,引入坐标法是解答的关键.
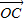 与
与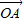 夹角为θ(0≤θ≤
夹角为θ(0≤θ≤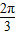 ),设
),设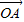 为直角坐标系的x轴,求出三个向量坐标,进而利用同角三角函数的平方关系,可得到x+y=2sin(θ+
为直角坐标系的x轴,求出三个向量坐标,进而利用同角三角函数的平方关系,可得到x+y=2sin(θ+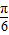 ),结合三角函数的图象和性质,可得答案.
),结合三角函数的图象和性质,可得答案.解答:
 解:记
解:记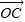 与
与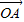 夹角为θ(0≤θ≤
夹角为θ(0≤θ≤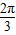 ),设
),设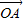 为直角坐标系的x轴.
为直角坐标系的x轴.则
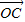 =(cosθ,sinθ),
=(cosθ,sinθ),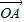 =(1,0),
=(1,0),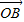 =(-
=(- ,
,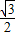 )
)代入
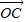 =x
=x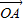 +y
+y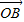 ,有(cos θ,sin θ)=(x,0)+(-
,有(cos θ,sin θ)=(x,0)+(-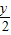 ,
,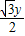 )
)联立方程组:x-
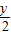 =cosθ,
=cosθ,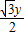 =sin θ
=sin θ故x+y=2sin(θ+
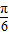 )
)∵0≤θ≤
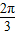 ,
,∴
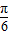 ≤θ+
≤θ+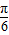 ≤
≤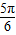
当θ+
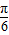 =
=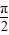 ,即θ=
,即θ=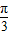 时,x+y取最大值2
时,x+y取最大值2当θ+
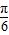 =
=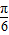 或
或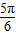 ,即θ=0<或
,即θ=0<或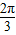 时,x+y取最小值1
时,x+y取最小值1故答案为:[1,2]
点评:本题考查的知识点是平面向量的基本定理及其意义,其中建立坐标系,引入坐标法是解答的关键.

练习册系列答案
相关题目

 ,其面积是2cm2则该扇形的周长是( )cm。
,其面积是2cm2则该扇形的周长是( )cm。