题目内容
【题目】已知椭圆
的左、右焦点分别为
，左、右顶点分别为
为直径的圆O过椭圆E的上顶点D，直线DB与圆O相交得到的弦长为
．设点
，连接PA交椭圆于点C，坐标原点为O．
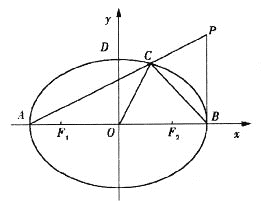
(I)求椭圆E的方程；
(II)若三角形ABC的面积不大于四边形OBPC的面积，求
的最小值．
【答案】（I）
；（II）
.
【解析】试题分析：(I)由直线与圆相交，利用垂径定理列方程求解即可；
（Ⅱ）分别求得三角形ABC的面积和四边形OBPC的面积，由题意即可求得|t|的最小值．
试题解析：
（Ⅰ）因为以
为直径的圆
过点
，所以
，则圆
的方程为
，
又
，所以
，直线
的方程为
，直线
与圆
相交得到的弦长为
，则
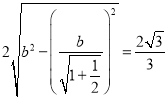，所以
， 
，
所以椭圆
的方程为
.
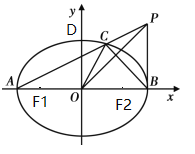
（Ⅱ）由已知得： 
， 
，椭圆方程为
，
设直线
的方程为
，由
整理得
，
解得： 
， 
，则点
的坐标是
，
故直线
的斜率为
，由于直线
的斜率为
，
所以
，所以
.
所以
，
，所以
，
整理得
， 
，所以
.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
目标测试系列答案
相关题目
【题目】某数学教师对所任教的两个班级各抽取20名学生进行测试，分数分布如表：
分数区间 | 甲班频率 | 乙班频率 |
[0，30） | 0.1 | 0.2 |
[30，60） | 0.2 | 0.2 |
[60，90） | 0.3 | 0.3 |
[90，120） | 0.2 | 0.2 |
[120，150） | 0.2 | 0.1 |
（Ⅰ）若成绩120分以上（含120分）为优秀，求从乙班参加测试的90分以上（含90分）的同学中，随机任取2名同学，恰有1人为优秀的概率；
（Ⅱ）根据以上数据完成下面的2×2列联表：在犯错概率小于0.1的前提下，你是否有足够的把握认为学生的数学成绩是否优秀与班级有关系？
优秀 | 不优秀 | 总计 | |
甲班 | |||
乙班 | |||
总计 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
P（K2≥k0） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
，其中n=a+b+c+d．
