题目内容
在平面内，已知
，
，
，设
，（
），则
等于
A． | B． | C． | D． |
B
解析试题分析：∵，∴
，又
,，根据平面向量基本定理可知m=1,n=，∴ =，故选B
点评：平面向量基本定理是向量运算的运用
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
下列式子正确的是( )
A． | B． |
C． ≤ | D． |
满足
，且关于
的函数
在实数集R上是单调递减函数，则向量
已知向量
，若
与
垂直，则
（ ）
A． | B． | C． | D．4 |
已知向量
的夹角为45°，且｜
｜＝1，｜2－
｜＝
，则｜｜＝
A．3 | B．2 | C． | D．1 |
已知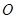
为平面上的定点，
、
、
是平面上不共线的三点，若
，则DABC是（ ）
| A．以AB为底边的等腰三角形 | B．以BC为底边的等腰三角形 |
| C．以AB为斜边的直角三角形 | D．以BC为斜边的直角三角形 |
向量
，
，若
与
平行，则
等于( )
A． | B． | C． | D． |
已知
三点的坐标分别是
，
，
，
，若
，则
的值为（ ）
A． | B． | C．2 | D． |
已知
是非零向量且满足
，
，则
与
的夹角是（ ）
A． | B． | C． | D． |