题目内容
已知 函数
函数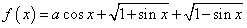 ,其中
,其中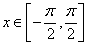 .
.
(1)设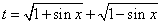 ,求
,求 的取值范围,并把
的取值范围,并把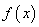 表示为
表示为 的函数
的函数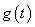 ;
;
(2)求函数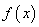 的最大值(可以用
的最大值(可以用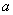 表示);
表示);
(3)若对区间 内的任意
内的任意 ,总有
,总有 ,求实数
,求实数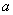 的取值范围.
的取值范围.
解:(1)因为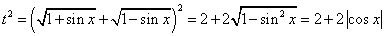 ,又因为
,又因为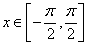 ,所以
,所以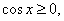 从而
从而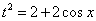 ,所以
,所以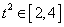 .又因为
.又因为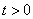 ,所以
,所以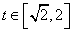 ,因为
,因为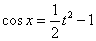 ,所以
,所以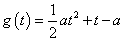 ,
,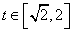 .-------4分
.-------4分
(2)求函数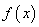 的最大值即求
的最大值即求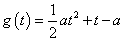 ,
,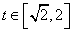 的最大值.
的最大值.
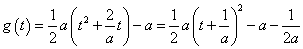 ,对称轴为
,对称轴为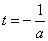 . --------5分
. --------5分
当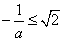 ,即
,即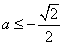 时,
时,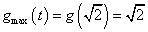 ;
;
当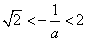 ,即
,即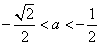 时,
时,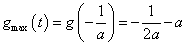 ;
;
当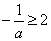 ,即
,即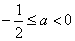 时,
时,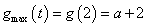 ; --------9分
; --------9分
综上, 当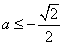 时,
时,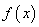 的最大值是
的最大值是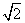 ;当
;当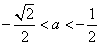 时,
时,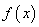 的最大值是
的最大值是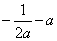 ;当
;当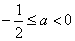 时,
时,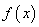 的最大值是
的最大值是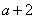 . ------- 10分
. ------- 10分
(3)要使得 对区间
对区间 内的任意
内的任意 恒成立,只需
恒成立,只需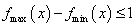 .也就是要求
.也就是要求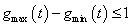 对
对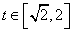 成立
成立
因为当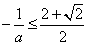 ,即
,即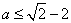 时,
时,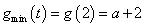 ;
;
且当 时,
时, 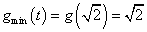 --------11分
--------11分
结合问题(2)需分四种情况讨论:
①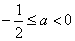 时,
时,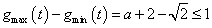 成立,所以
成立,所以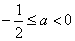 ;
;
②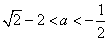 时
时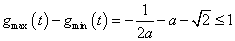 ,即
,即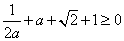 ,注意到函数
,注意到函数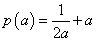 在
在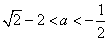 上单调递减,故
上单调递减,故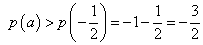 ,于是
,于是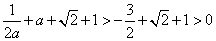 成立,所以
成立,所以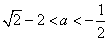
③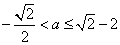 时
时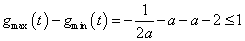 ,即
,即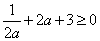 ,注意到函数
,注意到函数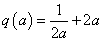 在
在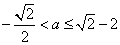 上单调递增,
上单调递增,
故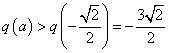 ,于是
,于是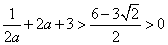 成立,所以
成立,所以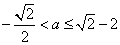 ;
;
④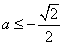 时,
时, ,即
,即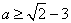 ,所以
,所以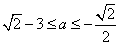 ; --------15分
; --------15分
综上,实数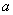 的取值范围是
的取值范围是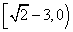 .
.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
 的二面角的棱上,有两个点
的二面角的棱上,有两个点 、
、 ,
, 、
、 分别是在这个二面角的两个半平面内垂直于
分别是在这个二面角的两个半平面内垂直于 的线段,且
的线段,且 ,
, ,
, ,
, 的长为 ;
的长为 ; 
 ,则
,则 = .
= .  ,圆心角为2
,圆心角为2 ,则该扇形的面积
,则该扇形的面积 为
为  .
. 为方程
为方程 的解集,集合
的解集,集合 为不等式
为不等式 的解集.
的解集. 时,求
时,求 ;
; ,求实数
,求实数 中,
中,  , 那么它的公差是
, 那么它的公差是


 _________.
_________.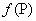 为双曲线
为双曲线 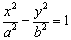 (a>0,b>0)上一点
(a>0,b>0)上一点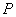 到它的两条渐近线的距离之和;当
到它的两条渐近线的距离之和;当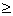
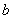 .则双曲线的离心率的取值范围是( )
.则双曲线的离心率的取值范围是( )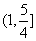 B.
B.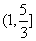 C.
C.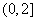 D.
D.
 -
- =-1的焦点为顶点,顶点为焦点的椭圆方程为( )
=-1的焦点为顶点,顶点为焦点的椭圆方程为( ) +
+ +
+ =1
=1 =1 D.
=1 D.