题目内容
【题目】如图,已知矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,将
的中点,将![]() 沿着
沿着![]() 折起,使得
折起,使得![]() .
.
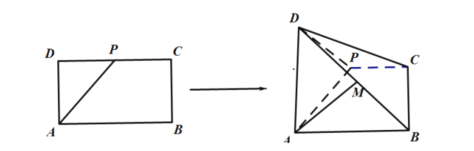
(1)求证:![]() ;
;
(2)若![]() 是
是![]() 的中点,求直线
的中点,求直线![]() 与平面
与平面![]() 的所成角的正弦值.
的所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)根据![]() ,
,![]() ,
,![]() 为
为![]() 的中点,在
的中点,在![]() 中,由勾股定理可得
中,由勾股定理可得![]() .由
.由![]() ,同理在
,同理在![]() 中,得到
中,得到![]() .由线面垂直的判定定理证明
.由线面垂直的判定定理证明![]() 面
面![]() 即可.
即可.
(2)结合(1)以![]() 为原点,
为原点,![]() 为
为![]() 轴,过
轴,过![]() 垂直于面
垂直于面![]() 方向为
方向为![]() 轴,建立空间直角坐标系,求得平面
轴,建立空间直角坐标系,求得平面![]() 的一个法向量
的一个法向量![]() 和
和![]() 的坐标,设直线
的坐标,设直线![]() 与平面
与平面![]() 的所成角
的所成角![]() ,由
,由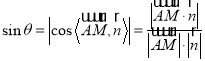 求解.
求解.
(1)因为![]() ,
,![]() ,
,![]() 为
为![]() 的中点,
的中点,
所以在![]() 中,
中,![]() ,
,
所以![]() .
.
又因为![]() ,
,
所以在![]() 中,因为
中,因为![]() ,
,
所以![]() .
.
又![]() ,
,
所以![]() 面
面![]() ,
,
又![]() 面
面![]() ,
,
所以![]() .
.
(2)以![]() 为原点,
为原点,![]() 为
为![]() 轴,过
轴,过![]() 垂直于面
垂直于面![]() 方向为
方向为![]() 轴,建立空间直角坐标系:
轴,建立空间直角坐标系:
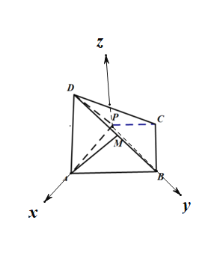
则![]() ,
,![]() ,
,![]() ,
,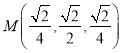 ,
,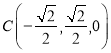 ,
,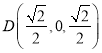 ,
,
所以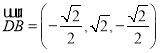 ,
,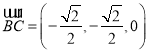 ,
,
设平面![]() 的一个法向量
的一个法向量![]() ,
,
则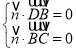 ,
,
即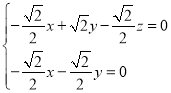 ,
,
令![]() ,则
,则![]()
所以平面![]() 的一个法向量为
的一个法向量为![]() ,
,
又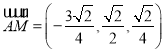 ,
,
设直线![]() 与平面
与平面![]() 的所成角
的所成角![]() ,
,
所以![]() 与面
与面![]() 所成角的正弦值为:
所成角的正弦值为: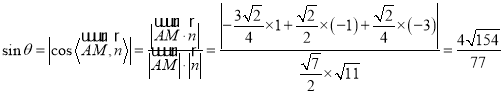 .
.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
【题目】为培养学生对传统文化的兴趣,某校从理科甲班抽取60人,从文科乙班抽取50人参加传统文化知识竞赛.
(1)根据题目条件完成下边![]() 列联表,并据此判断是否有99%的把握认为学生的传统文化知识竞赛成绩优秀与文理分科有关.
列联表,并据此判断是否有99%的把握认为学生的传统文化知识竞赛成绩优秀与文理分科有关.
优秀人数 | 非优秀人数 | 总计 | |
甲班 | |||
乙班 | 20 | ||
总计 | 60 |
(2)现已知![]() ,
,![]() ,
,![]() 三人获得优秀的概率分别为
三人获得优秀的概率分别为![]() ,
,![]() ,
,![]() ,设随机变量
,设随机变量![]() 表示
表示![]() ,
,![]() ,
,![]() 三人中获得优秀的人数,求
三人中获得优秀的人数,求![]() 的分布列及期望
的分布列及期望![]() .
.
附: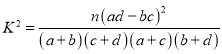 ,
,![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |