题目内容
设f(n)=cos(
+
),则f(1)+f(2)+f(3)+…+f(1998)=( )
| nπ |
| 2 |
| π |
| 4 |
A、
| ||||
B、-
| ||||
| C、0 | ||||
D、
|
分析:求出周期表,再确定达式在n=1,2,3,4时的函数值,然后解答即可.
解答:解:f(n)=cos(
+
),T=
=4,
把n=1,2,3,4代入f(n)=cos(
+
),
f(1)=cos(3/4π)=-
,
f(2)=cos(5/4π)=-
f(3)=cos(7/4π)=
,
f(4)=cos(9/4π)=
,
可以看出都是-
,-
,
,
交替出现,四个一个周期,和为0,把所有结果项相加等于-
-
=-
故选B
| nπ |
| 2 |
| π |
| 4 |
| 2π | ||
|
把n=1,2,3,4代入f(n)=cos(
| nπ |
| 2 |
| π |
| 4 |
f(1)=cos(3/4π)=-
| ||
| 2 |
f(2)=cos(5/4π)=-
| ||
| 2 |
f(3)=cos(7/4π)=
| ||
| 2 |
f(4)=cos(9/4π)=
| ||
| 2 |
可以看出都是-
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
故选B
点评:本题考查三角函数的周期的求法,考查计算能力,是基础题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
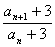 求使不等式cos(mπ)[f(2m2)-f(m)]≤0成立的正整数m的取值范围.
求使不等式cos(mπ)[f(2m2)-f(m)]≤0成立的正整数m的取值范围.