题目内容
已知数列{an}的前n项和为Sn,a1=1,Sn=an+1-3n-1,n∈N*.(1)证明数列{an+3}是等比数列;
(2)对k∈N*,设f(n)=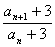 求使不等式cos(mπ)[f(2m2)-f(m)]≤0成立的正整数m的取值范围.
求使不等式cos(mπ)[f(2m2)-f(m)]≤0成立的正整数m的取值范围.
解:(1)由Sn=an+1-3n-1,则Sn-1=an-3(n-1)-1(n≥2),
两式相减并整理,得an+1=2an+3(n≥2),
即![]() =2(n≥2),又n=1时,a2=5,
=2(n≥2),又n=1时,a2=5,![]() =2.
=2.
∴数列{an+3}是首项为4,公比为2的等比数列.6分
(2)由(1)知an+3=4·2n-1=2n+1,
Sn=an+1-3n-1=2n+2-3n-4,
∴f(n)=
①当m为偶数时,cos(mπ)=1,f(2m2)=2m2+1,f(m)=m+1,
∴原不等式可化为(2m2+1)-(m+1)≤0,
即2m2-m≤0.故不存在符合条件的m.
②当m为奇数时,cos(mπ)=-1,f(2m2)=2m2+1,f(m)=2m+1-1,
∴原不等式化为2m2+1-2m+1+1≥0,
即2m2+2≥2m+1.
当m=1或3时不等式成立;
当m≥5时,2m+1-1=2(1+1)m-1=2(![]() +
+![]() +
+![]() +…+
+…+![]() +
+![]() )-1≥2m2+2m+3>2m2+1.
)-1≥2m2+2m+3>2m2+1.
∴m≥5时原不等式无解.
综合,得当m=1或3时,不等式cos(mπ)[f(2m2)-f(m)]≤0成立.

练习册系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |