题目内容
某校50名学生参加智力答题活动,每人回答3个问题,答对题目个数及对应人数统计结果见下表:
| 答对题目个数 | 0 | 1 | 2 | 3 |
| 人数 | 5 | 10 | 20 | 15 |
(Ⅰ)从50名学生中任选两人,求两人答对题目个数之和为4或5的概率;
(Ⅱ)从50名学生中任选两人,用X表示这两名学生答对题目个数之差的绝对值,求随机变量X的分布列及数学期望EX.
(Ⅰ)
(Ⅱ)X 0 1 2 3 P 




解析试题分析:(Ⅰ)先利用排列组合知识求出答对题目个数之和为4或5的人数,再利用古典概型知识求解;(Ⅱ)先写出X的可能取值,再求相应的概率,写成分布列,最后利用公式求期望值.
试题解析:(Ⅰ)记“两人答对题目个数之和为4或5”为事件A,则 (3分)
(3分) , (5分)
, (5分)
即两人答对题目个数之和为4或5的概率为 (6分)
(6分)
(Ⅱ)依题意可知X的可能取值分别为0,1,2,3.
则 (7分)
(7分) (8分)
(8分) (9分)
(9分) (10分)
(10分)
从而X的分布列为:
X的数学期望X 0 1 2 3 (11分) P 



 (12分)
(12分)
考点:1.离散型随机变量的分布列及期望;2.古典概型;3.排列组合.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在某次测验中,有6位同学的平均成绩为75分.用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学的成绩如下:1,2,3,4,5
| 编号n | 1 | 2 | 3 | 4 | 5 |
| 成绩xn | 70 | 76 | 72 | 70 | 72 |
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
(注:方差s2=
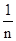 [(x1-
[(x1- )2+(x2-
)2+(x2- )2+…+(xn-
)2+…+(xn- )2],其中
)2],其中 为x1,x2,…,xn的平均数)
为x1,x2,…,xn的平均数) 某经销商试销A、B两种商品一个月(30天)的记录如下:
| 日销售量(件) | 0 | 1 | 2 | 3 | 4 | 5 |
| 商品A的频数 | 2 | 5 | 7 | 7 | 5 | 4 |
| 商品B的频数 | 4 | 4 | 6 | 8 | 5 | 3 |
(Ⅰ)求B商品日销售量不超过3件的概率;
(Ⅱ)由于某种原因,该商家决定只选择经销A、B商品的一种,你认为应选择哪种商品,说明理由。
某小组共有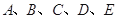 五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)如下表所示:
五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)如下表所示:
| | A | B | C | D | E |
| 身高 | 1.69 | 1.73 | 1.75 | 1.79 | 1.82 |
| 体重指标 | 19.2 | 25.1 | 18.5 | 23.3 | 20.9 |
(2)从该小组同学中任选2人,求选到的2人的身高都在1.70以上且体重指标都在[18.5,23.9)中的概率.
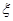 为取得红球的个数.
为取得红球的个数. 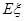 .
.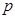 ,获得50元奖金的概率为
,获得50元奖金的概率为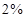 .
. ,求
,求 、
、 、
、 三个局商上任,求
三个局商上任,求 小时收费
小时收费 元,超过
元,超过 元(不足
元(不足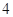 小时.
小时. 小时的概率为
小时的概率为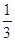 ,停车付费多于
,停车付费多于 元的概率为
元的概率为 ,求甲停车付费恰为
,求甲停车付费恰为 元的概率.
元的概率.