题目内容
已知圆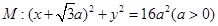 及定点
及定点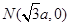 ,点
,点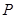 是圆
是圆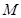 上的动点,点
上的动点,点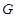 在
在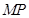 上,且满足
上,且满足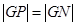 ,
,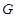 点的轨迹为曲线
点的轨迹为曲线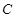 。
。
(1)求曲线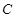 的方程;
的方程;
(2)若点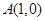 关于直线
关于直线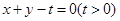 的对称点在曲线
的对称点在曲线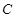 上,求
上,求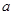 的取值范围。
的取值范围。
【答案】
(1) ;(2)
;(2) 。
。
【解析】
试题分析:(1)本小题首先根据题中的几何条件建立动点与两个定点的距离之和为定值 然后结合椭圆的定义可知动点的轨迹为椭圆,并可求得其方程为
然后结合椭圆的定义可知动点的轨迹为椭圆,并可求得其方程为 ;
;
(2)本小题首先求得点 关于直线
关于直线 的对称点
的对称点 ,再根据点
,再根据点 在椭圆
在椭圆 :
: 上,则可得
上,则可得 ,然后利用关于
,然后利用关于
 的一元二次方程有正根得到对称轴为
的一元二次方程有正根得到对称轴为 、
、 ,解得
,解得 (注意
(注意 这一条件)
这一条件)
试题解析:(1)设 ,
,
∵
∴
由椭圆定义得:曲线 的方程为
的方程为 5分
5分
(2)设 关于直线
关于直线 的对称点为
的对称点为 ,则
,则
 ,∴
,∴ 7分
7分
∴ ,
,
∵ 在曲线
在曲线 :
: 上,
上,
∴ ,
,
化简得: , 9分
, 9分
∵此方程有正根,令 其对称轴为
其对称轴为 ,
,
∴ ,
,
∴ ,
,
∵ ,∴
,∴ 。 12分
。 12分
考点:1 椭圆的定义;2 一元二次方程

练习册系列答案
相关题目
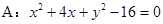 及定点
及定点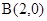 ,点Q是圆A上的动点,点G在BQ上,点P在QA上,且满足
,点Q是圆A上的动点,点G在BQ上,点P在QA上,且满足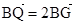 ,
,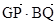 =0.
=0.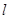 与曲线C交于M、N两点,直线
与曲线C交于M、N两点,直线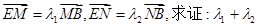 为定值。
为定值。